ipercubi
Come spezzare un ipercubo in due ciambelle
Immaginiamo di essere una formica su un cubo; la formica è al centro di una delle sei facce quadrate, parte in direzione del centro di una delle 4 facce adiacenti, e poi va “sempre dritto”. (Abbiamo messo “sempre dritto” tra virgolette perché la formica non si muove lungo una retta; è vincolata infatti a muoversi lungo la superficie del cubo quindi ogni tanto ci sono degli angoli retti nel suo percorso.)
ipercubi
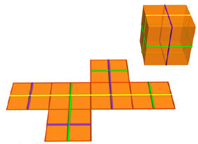
Gli sviluppi dell'ipercubo
Quando guardiamo una figura come questa e diciamo che si tratta di un ipercubo, facciamo naturalmente un atto di astrazione; e per poter riconoscere in questa figura le caratteristiche dell’ipercubo dobbiamo chiarire QUALE tipo di astrazione stiamo compiendo. Si tratta dello sviluppo di un ipercubo, quindi di un oggetto 3d il cui rapporto con il “vero” ipercubo in 4d è analogo al rapporto che c’è fra questa figura piana di sei quadrati e un cubo.