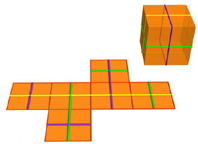
Let us imagine to be an ant on a cube. The ant is in the middle of one of the six square faces. It moves toward the center of one of the four adjacent faces and, after that, it goes “straight ahead”. “Straight ahead” is in inverted commas because the ant does not move on a straight line. It must move on the surface of the cube, so sometimes there are right angles on its path.
It is easy to realize that the ant goes back to the starting point after moving on four squares which form a sort of a “ring”. The four squares are all the faces of the cube except two, which are opposite one to the other.
On a cube there are three different rings like the one mentioned before.
What happens on a hypercube? What kind of path will a hyper-ant describe if it starts from the center of one of the eight cubic faces and goes “straight ahead” aiming at the center of one of the six adjacent cubes?

The path described by the hyper-ant closes up this time as well. The hyper-ant goes back to the starting point after passing on four cubes. The chain of four cubes can be visualized quite well on a net of the hypercube. In particular, it is clearer on a net where there are four cubes one over the other. When we make all the identifications and pass to the four-dimensional world, we must recall that, on the column of four cubes, the bottom face of the bottom cube is glued to the upper face of the upper cube. In this way, the four cubes form a doughnut. Surprisingly, the cubes “avoided” by the ant form a doughnut too, which is linked to the previous one. This can be well visualized in some nets of the hypercube. This means that the hypercube splits in two linked doughnuts, each of four cubes.

How many doughnuts of this kind are there in a hypercube? We can start from a cube and point out that there is a doughnut - which contains the cube - for each of the three directions orthogonal to two opposite faces in the cube. Since there are 8 cubes, we obtain 24= 8 × 3 doughnuts. Each of these doughnuts is counted 4 times, one for each of the cubes in it. In other words, there are six different doughnuts in a hypercube.

In the animation about the hyper-ant you can see the six different possible paths, that is to say, the six possible doughnuts of four cubes in a hypercube (and the three possible decomposition of a hypercube in two pairs of doughnuts). On the left of the screen, the “environment” of the hypercube is described under stereographic projection.The hypercube is enflated on a hypersphere which is next projected on three-dimensional space. On the right of the screen, you can follow the same paths on a net of the hypercube. The colours are not randomly chosen. They highlight the directions of the two-faces. The 24 squares in the hypercube are coloured with six different colours; for each colour there are 4 (parallel) faces which are coloured with that colour. The six possible paths of the hyper-ant correspond to the six different colours, i.e., each of them is “orthogonal” to the 4 squares of a fixed colour.