Tutti sono d’accordo sul fatto che sia “equo” usare il cubo, o anche uno degli altri poliedri regolari, per giocare a dadi, perché ogni faccia ha la stessa probabilità di apparire, o, come si dice, le facce sono indistinguibili. Ma che cosa vuol dire esattamente “indistinguibili”?
L’aggettivo sta a indicare che se abbiamo un poliedro regolare e ne fissiamo due facce, riusciamo sempre a ruotarlo in modo che la prima faccia vada ad occupare la posizione iniziale della seconda e globalmente il poliedro torni su se stesso.
Ad esempio, per spostare nella faccia in alto la faccia del cubo che qui in figura è di fronte, basta ruotare il cubo di 90° intorno alla retta segnata come r in figura. Le due facce, quindi, non si possono distinguere se non sono state marcate con un’etichetta.
La stessa cosa accade anche per due vertici o per due spigoli: per mandare lo spigolo a nello spigolo b basta ruotare il cubo di 120° intorno alla retta s; e la stessa rotazione può servire anche per mandare il vertice P nel vertice Q.

La tabella qui sotto descrive i cinque poliedri regolari.

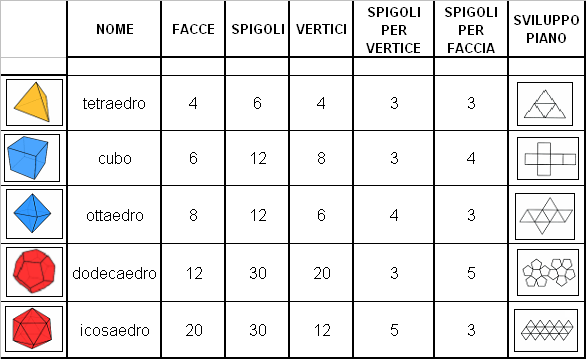
In essa le prime tre colonne numeriche riportano il numero di facce, di spigoli, e di vertici per ciascuno di essi, mentre le due successive possono essere interpretate come le “istruzioni” per costruire lo scheletro del poliedro se si hanno a disposizione bastoncini tutti di uguale lunghezza e un modo per unirli insieme nei loro estremi (ad esempio, se si hanno cannucce da bibita e scovolini nettapipe per fare i giunti). Così i numeri che compaiono nell’ultima riga indicano che in un icosaedro ci sono 20 facce, 30 spigoli, 12 vertici, 5 spigoli in ogni vertice e 3 spigoli per ogni faccia: se continuiamo a unire cinque cannucce in ogni vertice e a formare dei triangoli, l’oggetto “si chiude” e dà origine proprio a un icosaedro.

Anche la colonna finale della tabella dà delle istruzioni per costruire il poliedro corrispondente: in questo caso partendo dal disegno dello sviluppo su un cartoncino si ottiene la superficie del poliedro e non solo lo scheletro.

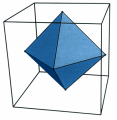
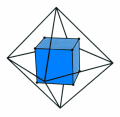
Ci sono altre informazioni che possiamo trarre dalla tabella. Ad esempio il fatto che cubo e ottaedro sono “parenti”: hanno lo stesso numero di spigoli, e l’uno non solo ha tante facce quanti sono i vertici dell’altro, ma anche per ogni suo vertice si contano tanti spigoli quanti sono quelli di una faccia dell’alt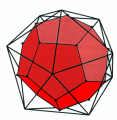ro. Questa parentela è messa in evidenza dalle figure qui accanto: se consideriamo i centri delle facce di un cubo e ne congiungiamo due quando le facce corrispondenti hanno uno spigolo in comune, otteniamo un ottaedro.
E, viceversa, se facciamo la stessa costruzione partendo da un ottaedro otteniamo un cubo.
Anche il dodecaedro e l’icosaedro sono parenti nel senso che si è appena detto, come si può osservare sia a partire dalle colonne numeriche della tabella sia nelle due figure qui accanto.

Invece di chi è “parente” il tetraedro? Non ci sono altri poliedri regolari, ma il fatto che il tetraedro regolare abbia tante facce quanti vertici può aiutarci a rispondere a questa domanda…

Tratto dalla scheda Ancora sui cinque poliedri regolari a cura di Cristina Vezzani per la mostra Simmetria, giochi di specchi.