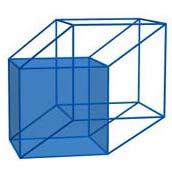
Lo sviluppo, il diagramma di Schlegel o la proiezione; quale dei tre rappresenta meglio l'ipercubo? La risposta è: dipende. In effetti tutti e tre sono delle rappresentazioni tridimensionali dell'ipercubo, e non sono l'ipercubo stesso. Una rappresentazione sarà più utile per studiare una data proprietà piuttosto che un'altra.

Per esempio, per vari problemi di natura combinatorica il diagramma di Schlegel appare la rappresentazione più idonea, mentre per alcuni problemi di minimo (come ad esempio trovare il cammino più breve tra due punti) si preferirà lo sviluppo. O ancora, il fatto che esistano un'infinità di cubi nell'ipercubo appare più evidente nella proiezione. Avere più rappresentazioni ci permette così di accedere a più informazioni sull'ipercubo e sulle sue proprietà.

Nello sviluppo, nel diagramma di Schlegel e nella proiezione “rappresentiamo” l'ipercubo nello spazio tridimensionale; se da un lato perdiamo l'aspetto quadridimensionale dell'ipercubo, dall'altro tali rappresentazioni, essendo tridimensionali, possono essere più facilmente studiate e manipolate.

In altre parole, invece di considerare l'ipercubo, ne studiamo un'immagine (più semplice) da cui deduciamo delle proprietà dell'ipercubo stesso.

Nello stesso modo i matematici hanno definito varie “rappresentazioni” dello spazio quadridimensionale, di diversa natura (algebrica, analitica...), più o meno complesse e più o meno difficili da manipolare, che permettono loro di osservare e descrivere varie caratteristiche dello spazio quadridimensionale.

Vale la pena comunque notare che, anche se sviluppo, diagramma di Schlegel e proiezione sono tutti e tre degli oggetti tridimensionali, lo sviluppo si differenzia dagli altri due, in quanto anche il diagramma di Schlegel è in realtà una proiezione. Se identifichiamo le facce come richiesto nello sviluppo dell’ipercubo, quello che otteniamo è realmente l'ipercubo; è solo che non possiamo farlo in pratica, visto che il nostro spazio è tridimensionale. Questo processo di costruire degli oggetti di dimensione più grande tramite identificazioni di facce, segmenti o punti (ovvero di oggetti di dimensione più piccola) è una tecnica molto usata in Topologia e che permette di costruire un'infinità di oggetti disparati a partire da figure semplici.

Per esempio, considerate un quadrato e identificatene le due coppie di lati opposti; immaginando il quadrato come elastico e deformabile potete realizzare queste identificazioni nello spazio tridimensionale e quello che ottenete è una ciambella.

Ma se in una delle due identificazioni date una mezza torsione prima di incollare i lati, in modo da scambiarne il verso, non solo non ottenete una ciambella, ma non è proprio possibile deformare il quadrato nello spazio tridimensionale, senza produrre delle autointersezioni.
E' invece possibile realizzare queste identificazioni nello spazio quadridimensionale. Questo oggetto è conosciuto col nome di bottiglia di Klein .

A cura di Paolo Bellingeri per la mostra Un tuffo nella quarta dimensione.