Immaginiamo di essere una formica su un cubo; la formica è al centro di una delle sei facce quadrate, parte in direzione del centro di una delle 4 facce adiacenti, e poi va “sempre dritto”. (Abbiamo messo “sempre dritto” tra virgolette perché la formica non si muove lungo una retta; è vincolata infatti a muoversi lungo la superficie del cubo quindi ogni tanto ci sono degli angoli retti nel suo percorso.)

È facile rendersi conto che la formica torna al punto di partenza dopo essere passata da 4 quadrati che formano una sorta di anello: si tratta di tutte le facce del cubo, salvo 2 facce opposte fra loro.
Esistono nel cubo 3 diversi anelli di questo tipo.
Cosa succede in un ipercubo? Che percorso compierà una iperformica che parte dal centro di una delle otto facce cubiche dell’ipercubo e si muove “sempre dritto” partendo in direzione del centro di uno dei sei cubi adiacenti?

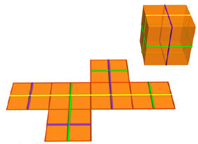
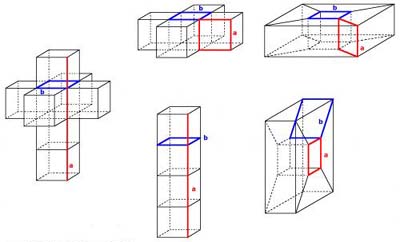
Anche questa volta il percorso si chiude su se stesso e la iperformica torna al punto di partenza dopo aver attraversato 4 cubi. L’anello dei 4 cubi attraversati dal percorso dell’iperformica si può visualizzare abbastanza bene su uno sviluppo dell’ipercubo, se in particolare, fra i tanti sviluppi, se ne sceglie uno in cui ci siano 4 cubi “in fila”: nella colonna di 4 cubi bisogna ricordare che la faccia inferiore del cubo più in basso si identifica, quando l’oggetto si richiude nel mondo 4d, alla faccia superiore del cubo più in alto. Sicché i 4 cubi formano un anello. Ma la cosa interessante è che anche i 4 cubi “esclusi” dal percorso della formica formano un anello, allacciato al precedente, il che si visualizza particolarmente bene in alcuni sviluppi dell’ipercubo, sicché l’ipercubo si spezza nell’unione di due ciambelle solide, formate da 4 cubi ciascuna, allacciate fra loro.

Quanti anelli di questo genere ci sono in un ipercubo? Possiamo partire da un cubo, e osservare che c’è un tale anello (che contiene il cubo fissato) per ognuna delle tre direzioni ortogonali a due facce opposte del cubo. I cubi sono 8 e quindi otteniamo in questo modo 24= 8 × 3 anelli, però ogni anello è stato in questo modo contato 4 volte, una per ciascuno dei 4 cubi che lo compongono, quindi in realtà gli anelli diversi in un ipercubo sono sei.

Nell’animazione dell’iperformica si possono vedere i sei diversi possibili percorsi dell’iperformica, ovvero individuare i sei possibili anelli di 4 cubi nell’ipercubo (e le tre diverse decomposizioni dell’ipercubo in due anelli allacciati). Sulla sinistra dello schermo, il “paesaggio” nell’ipercubo è descritto tramite proiezione stereografica: l’ipercubo è gonfiato su un’ipersfera che poi viene proiettata nello spazio 3d. Sulla destra dello schermo, si seguono invece gli stessi percorsi su uno sviluppo dell’ipercubo. I colori non sono messi a caso, ma mettono in evidenza le direzioni delle 2-facce: i 24 quadrati che compongono l’ipercubo sono colorati con 6 colori diversi e per ogni colore ci sono 4 facce (fra loro parallele) colorate con quel colore. I sei possibili percorsi dell’iperformica corrispondono a questi sei colori, nel senso che ciascuno è ortogonale ai 4 quadrati di un determinato colore.