Esagoni sulla carta a quadretti
Esagoni sulla carta a quadretti
Non è possibile disegnare un esagono regolare sulla carta a quadretti.
Per giustificarlo, cominciamo a far vedere che non è possibile disegnare un triangolo equilatero sulla carta a quadretti, o, equivalentemente, costruirlo sul geopiano.
Infatti, se fosse possibile, troveremmo 3 vertici P,Q,R della quadrettatura tali che i tre segmenti PQ, QR, PR siano della stessa lunghezza.
Possiamo immaginare un riferimento cartesiano, con l'origine nel punto P, gli assi paralleli alle rette della quadrettatura e l'unità di misura corrispondente al lato di un quadretto. Rispetto a questo sistema di riferimento il punto Q avrà coordinate (a,b) espresse da due numeri interi e così anche il punto R=(c,d), mentre naturalmente P=(0,0). Applichiamo ora il teorema di Pitagora per esprimere l'uguaglianza dei tre segmenti PQ, QR, PR (anzi, l'uguaglianza dei loro quadrati). Avremo che:
a2+b2=c2+d2=(c-a)2+(d-b)2.
Sviluppando l'ultimo membro si ottiene
a2+b2=c2+d2=2(ac+bd)
e a questo punto possiamo ricordarci del fatto che a,b,c,d sono tutti numeri interi.
Allora a2+b2 è un numero pari, il che significa che a e b sono entrambi pari oppure entrambi dispari, ma non possono essere uno pari e uno dispari (e lo stesso ragionamento si può applicare ai due numeri c e d).
Supponiamo che a e b siano entrambi dispari: in tal caso a2+b2 è un numero pari, ma non è multiplo di 4, quindi ac+bd è un numero dispari; ricordando che a e b sono dispari, questo significherebbe che c e d dovrebbero essere uno pari e uno dispari, mentre sappiamo che questo non è possibile.
L'unica eventualità che ci resta è che a e b siano entrambi pari, e così anche c e d. Ma se tutti questi numeri sono pari, potremmo costruire un triangolo equilatero più piccolo, con vertici nei punti
P=(0,0), Q=(a/2,b/2), R=(c/2,d/2), e su questo triangolo potremmo ripetere il ragionamento fatto fin qui, ottenendone uno ancora più piccolo ... e così via all'infinito.
Ma questo naturalmente è un assurdo perché, se esiste la possibilità di disegnare un triangolo equilatero sulla carta a quadretti, ci sarebbe anche fra questi triangoli equilateri uno di grandezza minima.
Per quanto riguarda poi l'impossibilità di costruire un esagono regolare, basta osservare che, se esistesse un esagono regolare con vertici nei vertici della quadrettatura, avremmo un triangolo equilatero con due vertici in due vertici consecutivi dell'esagono e il terzo nel centro dell'esagono; quest'ultimo punto potrebbe non essere un vertice della quadrettatura, ma, in tal caso, basta raddoppiare tutti i lati dell'esagono e ne otteniamo un altro per il quale il centro è nei vertici della quadrettatura e quindi otterremmo un triangolo equilatero con vertici nella quadrettatura, il che sappiamo essere impossibile.
Appurato che questi poligoni non si possono disegnare sulla carta a quadretti, possiamo però cercarne delle buone approssimazioni; ad esempio, il triangolo con vertici nei punti (con le stesse convenzioni di cui sopra) di coordinate P=(0,0), Q=(3,3), R=(4,-1) non è equilatero, ma è una buona approssimazione di un triangolo equilatero perché un lato misura 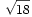 e gli altri due
e gli altri due 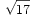 ; e a partire da questo triangolo "quasi" equilatero è facile poi disegnare un esagono "quasi" regolare, o anche un dodecagono "quasi" regolare, o ...
; e a partire da questo triangolo "quasi" equilatero è facile poi disegnare un esagono "quasi" regolare, o anche un dodecagono "quasi" regolare, o ...