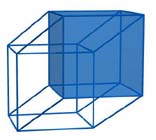
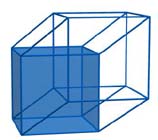
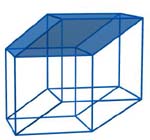
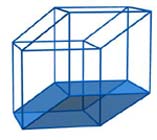
In each representation of a hypercube you should “see” each of the eight cubic faces of the hypercube. This is clear for a net, but what about a Schlegel diagram and a projection? Where are the eight cubes?

In a Schlegel diagram, you can see that seven out of the eight cubic faces of a hypercube are represented. A small cube inside and other six deformed cubes - which are glued face to face - and form the big cube outside. Where is the eighth cube? The faces of the eighth cube are the faces of the big cube. Since the interior of the big cube is already “taken” by the other seven cubes, we can imagine that the interior of the eighth cube is the exterior of the big cube, which is an unlimited region!
This remark comes from our way of thinking in three dimensional space. The Schlegel diagram of the cube in the plane can help us understand the hypercube.
We notice that also in a Schlegel diagram of a cube a face is missing. It is the face delimited by the big square. Actually, this is a two-dimensional projection. In fact, we should realize that the other five faces are in close-up (like a relief) with respect to the sixth face, the one delimited exactly by the edges of the big square.
Likewise, in the diagram of a hypercube the seven cubes, which are inside, must be imagined in “close-up” with respect to the cubic face delimited by the big cube. This perspective is less evident than in the case of a cube because we are adding a dimension to our three-dimensional space to highlight what is in the big cube; but this is “watching” in a four-dimensional space…
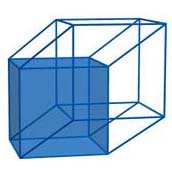
As for a perspective projection of a hypercube two cubes are easily detectable. Where are the others? Let us consider a projection of a cube on the plane. The projection of the six faces are intertwined. In the same vein, the projection of the eight cubic faces of a hypercube intersect each other. To observe them, let us consider the bases of these two cubes.

You can easily see that they are the bases of two other solids (first, second) with eight vertices and twelve edges, which are the projection of two other cubic faces.
There are still four cubes missing: we leave it to the reader to discover where they are “hidden”……