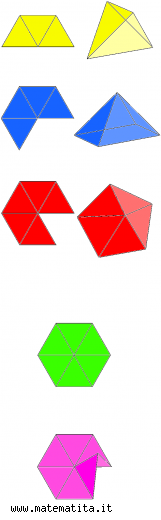
i cinque poliedri regolari
I cinque poliedri regolari
Quando lanciamo un dado, ci aspettiamo che, data l’evidente simmetria della sua forma, ognuno dei sei numeri segnati sulle facce abbia la stessa probabilità di uscire.
Nei negozi di giochi, oltre all’usuale dado a sei facce, si vendono anche dadi con quattro, otto, dodici e venti facce.
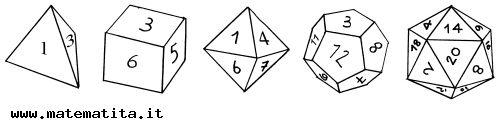
Per vedere che cosa hanno di particolare i cinque poliedri rappresentati da questi dadi, consideriamo qualche altro esempio di poliedro.

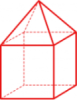

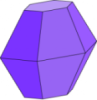
i cinque poliedri regolari
Perché solo cinque?
Per costruire un poliedro regolare, dobbiamo prendere tante copie dello stesso poligono regolare e unirle lungo gli spigoli (in modo che ci sia sempre lo stesso numero di copie intorno a un vertice). Quante sono le possibilità?
Incominciamo a cercare i poliedri regolari con facce triangolari. Se mettiamo insieme tre triangoli equilateri intorno a uno stesso vertice, otteniamo il tetraedro; se ne mettiamo quattro, ritroviamo l’ottaedro e se ne mettiamo cinque, generiamo l’icosaedro. Sei triangoli equilateri che concorrono in un vertice sono troppi perché stanno su uno stesso piano, mentre se se ne mettono insieme sette o più si ottiene necessariamente un solido concavo; quindi non ci possono essere altri poliedri regolari con facce triangolari. Passiamo ai quadrati. Possiamo costruire soltanto il cubo mettendo insieme tre quadrati in ogni vertice, dal momento che quattro quadrati sono già troppi perché stanno su uno stesso piano. Con i pentagoni regolari possiamo costruire solo il dodecaedro, prendendone tre per vertice, perché il pentagono regolare ha gli angoli così grandi che quattro sono troppi.
i cinque poliedri regolari
Ancora sui cinque poliedri regolari
Tutti sono d’accordo sul fatto che sia “equo” usare il cubo, o anche uno degli altri poliedri regolari, per giocare a dadi, perché ogni faccia ha la stessa probabilità di apparire, o, come si dice, le facce sono indistinguibili. Ma che cosa vuol dire esattamente “indistinguibili”?
L’aggettivo sta a indicare che se abbiamo un poliedro regolare e ne fissiamo due facce, riusciamo sempre a ruotarlo in modo che la prima faccia vada ad occupare la posizione iniziale della seconda e globalmente il poliedro torni su se stesso.
Ad esempio, per spostare nella faccia in alto la faccia del cubo che qui in figura è di fronte, basta ruotare il cubo di 90° intorno alla retta segnata come r in figura. Le due facce, quindi, non si possono distinguere se non sono state marcate con un’etichetta.
La stessa cosa accade anche per due vertici o per due spigoli: per mandare lo spigolo a nello spigolo b basta ruotare il cubo di 120° intorno alla retta s; e la stessa rotazione può servire anche per mandare il vertice P nel vertice Q.