Quando lanciamo un dado, ci aspettiamo che, data l’evidente simmetria della sua forma, ognuno dei sei numeri segnati sulle facce abbia la stessa probabilità di uscire.
Nei negozi di giochi, oltre all’usuale dado a sei facce, si vendono anche dadi con quattro, otto, dodici e venti facce.

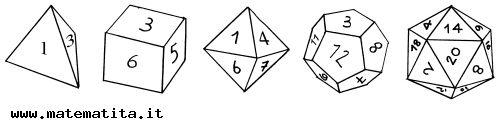
Per vedere che cosa hanno di particolare i cinque poliedri rappresentati da questi dadi, consideriamo qualche altro esempio di poliedro.

        

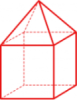
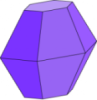
Anche con un geoide, ad esempio, potremmo costruire un dado. Questo poliedro potrebbe anche a prima vista sembrare più “regolare” dei cinque dadi iniziali dato che ha una forma che si avvicina meglio a una sfera ma, guardandolo con attenzione, ci accorgiamo che i suoi vertici non sono tutti dello stesso tipo: da alcuni, come da A, escono cinque spigoli e quindi vi si incontrano cinque poligoni, da altri, come da B, escono sei spigoli e quindi vi si incontrano sei poligoni.

Chiamiamo regolare un poliedro se le sue facce sono poligoni regolari uguali fra loro e in ogni vertice arriva lo stesso numero di facce. In un poliedro di questo tipo sia le facce che gli spigoli che i vertici sono indistinguibili.

Nessuno dei poliedri illustrati qui sopra è quindi regolare, mentre i cinque dadi sono esempi di poliedri regolari. Ce ne sono altri? (dopotutto nel piano possiamo costruire poligoni regolari con quanti lati vogliamo). No, nello spazio esistono solo i cinque poliedri regolari rappresentati in questi dadi.

Già gli antichi Greci erano a conoscenza di questo fatto e ne furono così impressionati che i Pitagorici e successivamente Platone costruirono le loro teorie cosmogoniche associando ai cinque poliedri regolari i costituenti fondamentali della natura. Per questo i poliedri regolari sono anche detti solidi platonici.
Nel “Timeo” Platone descrive il tetraedro come “elemento e germe” del fuoco, l’ottaedro dell’aria, l’icosaedro dell’acqua, il cubo della terra, mentre il dodecaedro rappresenta l’immagine dell’universo nella sua totalità: “rimanendo una quinta combinazione, Dio se ne giovò per il disegno dell’universo”.
L’ultimo libro degli “Elementi” di Euclide è dedicato ai cinque solidi platonici, ad alcune loro proprietà e relazioni e alla dimostrazione del fatto che non ne esistono altri.
Sono stati ritrovati modelli di poliedri regolari anche in civiltà precedenti a quella greca, e il loro fascino, legato sia all’armonia delle proporzioni che alle proprietà matematiche, ha continuato a colpire artisti e scienziati fino ai giorni nostri.
I dodecaedri avevano un significato religioso anche nella cultura etrusca ed erano usati come dadi nell’Italia romana.
Nel Rinascimento italiano i poliedri regolari sono stati un ottimo soggetto su cui compiere studi prospettici: li ritroviamo in opere per esempio di Paolo Uccello, Piero della Francesca, Albrecht Dürer, Leonardo da Vinci, Luca Pacioli e Leonardo Pisano (il Fibonacci).

Keplero nel 1595 credette di “essere penetrato nei segreti del creatore” poiché aveva elaborato un modello di sistema planetario (poi rivelatosi errato) utilizzando i solidi platonici per descrivere le distanze tra le orbite ellittiche dei sei pianeti allora conosciuti.

Forme ispirate ai poliedri regolari abbondano anche nell'arte e nel design moderni, dalle opere di Escher all'architettura modulare, agli oggetti di Munari.
Una curiosità tra le tante: in Francia sono stati costruiti cassonetti per la raccolta differenziata a forma di dodecaedro.

Anche la natura ci mostra esempi di poliedri regolari: alcuni cristalli, la forma tetraedrica della schiuma della birra, i virus che hanno spesso forma icosaedrica, semplici organismi viventi come i radiolari, ...

Tratto dalla scheda I cinque poliedri regolari a cura di Cristina Vezzani per la mostra Simmetria, giochi di specchi.