Se osserviamo la disposizione delle foglie sul fusto di una pianta, sia essa erbacea o arborea, possiamo meravigliarci nello scoprire la regolarità con cui queste sono disposte.

Anche se tale fenomeno appare maggiormente evidente in molte specie provviste di due foglie per nodo, se consideriamo quelle che possiedono solo una foglia in ciascun nodo (pensiamo alla comune canna di palude) possiamo, in alcuni casi, trovare una disposizione degli elementi fogliari la cui regolarità si può descrivere e esprimere in termini matematici.

In Figura 10 i punti che corrispondono alle foglie si immaginano sulla superficie di un cono (che dà ragione del fatto che il diametro del fusto delle piante sia erbacee che arboree diminuisce andando verso l'apice vegetativo).
Possiamo costruire un modello immaginando, ad esempio, di avere unito le foglie con una linea (bianca in figura), iniziando dalla più bassa (che chiamiamo n°0) percorrendo il fusto verso l'alto e fermandoci quando abbiamo incontrato un'altra foglia sulla stessa direttrice del cono.

Osserviamo ancora la Figura 10: se abbiamo disegnato una linea con andamento a elica attorno al modello di fusto di una pianta (come in figura) e l'abbiamo proiettato su un piano - che potrebbe essere un foglio di carta – BENE, abbiamo ottenuto una spirale.

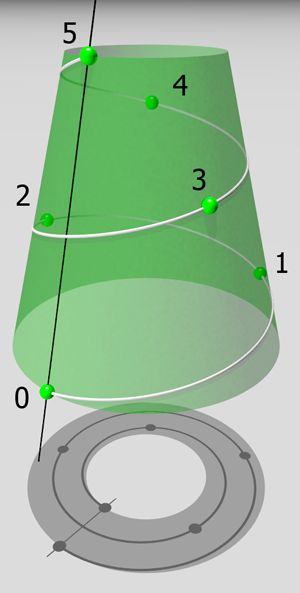
Cercando di contare quanti giri di elica percorriamo per intercettare due foglie poste sulla stessa verticale, che nella figura sono la numero 0 e la numero 5, ci rendiamo conto che dovremo percorrere il fusto con due giri prima di giungere alla foglia n°5.

Questi numeri possono essere espressi tramite una frazione, detta frazione fillotassica, N/D dove N rappresenta il numero di giri di spirale e D il numero delle foglie intercettate (la foglia da cui parte il conteggio è la numero zero).

NEL NOSTRO ESEMPIO LA FRAZIONE FILLOTASSICA RISULTA: 2/5

La frazione N/D possiede un importante significato in quanto (interpretata come frazione di 360°) rappresenta l'angolo di divergenza, ovvero l'angolo individuato dalle proiezioni (su un piano perpendicolare al fusto) delle semirette corrispondenti a due foglie consecutive.

La funzione di tale regolare disposizione è quella di permettere alle foglie, posizionate a diversi livelli, di ombreggiarsi il meno possibile l'una con l'altra e di conseguenza di ottenere una maggiore captazione della luce solare.

Per calcolare il valore dell'angolo, si moltiplica 360° (angolo giro in gradi) per la frazione che abbiamo trovato; nel caso rappresentato in Figura 1 si ottiene:

360° x 2/5 = 144°.

Naturalmente questo valore si riferisce al caso particolare che abbiamo preso come esempio; nella realtà ogni specie vegetale possiede il proprio grado di fillotassi, e quindi la frazione fillotassica e l'angolo di divergenza sono differenti per specie diverse.

Le frazioni N/D che si riscontrano più frequentemente in natura sono:

1/2    1/3    2/5    3/8    5/13    8/21    13/34    21/55...

Se osserviamo attentamente queste frazioni noteremo che il numeratore (e il denominatore) di ciascuna di esse è la somma dei due numeratori (rispettivamente dei due denominatori) precedenti, e che la sequenza dei numeratori (e anche quella dei denominatori, traslata) corrisponde alla successione di numeri di Fibonacci: 1, 1, 2, 3, 5, 8, 13, 21 ecc.

La successione è infinita (anche se naturalmente nei vegetali si riscontrano solo i primi termini): a mano a mano che aumentano i valori N e D, il valore della frazione si avvicina al numero 0,381966…

Tale numero è collegato al RAPPORTO AUREO τ, che è quel numero positivo caratterizzato dal fatto che τ²= τ+1.

Precisamente , all'aumentare dei valori di N e D la frazione N/D si avvicina a 1/(1 +τ ).

Moltiplicando 360° per 0,381966 otteniamo l'angolo limite di divergenza che corrisponde a 137°30'28", ovvero l'angolo ideale che permetterebbe a tutte le foglie di disporsi in modo da ottenere la massima quantità di luce solare indispensabile per la fotosintesi.

Fig. 11 - Helianthus annuus

Referenze iconografiche

fotografie 1-2-4-6-7-8: Giovanna Angelucci
fotografie 3-5: Centro matematita
fotografia 9: ©Franco Valoti
disegni di Giovanna Angelucci
figura 10: immagine realizzata da Riccardo Moschetti
figura 11: Centro matematita
fotografie di copertina e ultima pagina: ©Franco Valoti