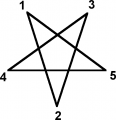Il primo disegno qui a lato raffigura un pentagono stellato, o pentagramma, un elemento decorativo noto fin dall’antichità e un simbolo in diverse culture. Esso è costituito da un usuale pentagono regolare circondato da cinque triangoli isosceli uguali, ottenuti prolungando i lati del pentagono di partenza, e può essere tracciato disegnando nell’ordine i cinque segmenti da 1 a 2, da 2 a 3, da 3 a 4, da 4 a 5, da 5 a 1 (questo è possibile perché i triangoli hanno l’altezza “giusta”:
se fossero più bassi oppure più alti, come nei disegni qui a lato, non sarebbe possibile ottenere la figura disegnando solo cinque segmenti).

Il pentagramma può essere considerato un pentagono regolare: infatti i cinque “lati” (i segmenti che abbiamo tracciato) sono di uguale lunghezza e gli angoli nei cinque “vertici” (i punti che abbiamo unito nell’ordine) hanno tutti la stessa ampiezza. Per distinguerlo dall’usuale pentagono regolare, viene chiamato pentagono regolare stellato.
Analogamente, esistono poligoni regolari stellati con sette, otto, nove, … lati (anzi, talvolta ne esistono di tipi diversi; perché?), mentre non esistono triangoli, quadrati o esagoni stellati (perché?).
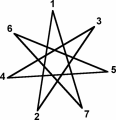
I disegni qui sotto rappresentano i due tipi possibili di ettagoni regolari stellati e l’unico tipo di ottagono regolare stellato.

.

È possibile fare qualcosa di simile con i poliedri regolari?
Estendendo gli spigoli di un tetraedro, di un cubo o di un ottaedro non si ottengono nuovi poliedri. Invece, a partire dal dodecaedro e dall’icosaedro, si ottengono i due poliedri della figura qui sotto.

Essi, a un primo sguardo, ci appaiono rispettivamente come un dodecaedro e un icosaedro sulle cui facce sono state costruite delle piramidi regolari tutte uguali tra loro; l’altezza di queste piramidi è quella “giusta” affinché i sessanta triangoli che ne sono le facce laterali a cinque a cinque stiano su uno stesso piano e circondino un pentagono insieme al quale formano un pentagramma (la colorazione nella figura precedente mette in evidenza uno di questi piani).

I due poliedri possono dunque essere ottenuti unendo nei vertici – a cinque a cinque oppure a tre a tre – dodici pentagoni regolari stellati tutti uguali, in modo che le “facce” siano unite l’una all’altra lungo i loro lati, come negli usuali poliedri, tuttavia si attraversino nascondendo alla vista i pentagoni centrali di ogni pentagramma. In questa interpretazione, essi sono dei poliedri regolari, più precisamente dei dodecaedri, detti rispettivamente piccolo dodecaedro stellato e grande dodecaedro stellato.
Da un punto di vista matematico, questi poliedri furono studiati per la prima volta intorno al 1600 dallo scienziato tedesco Keplero (1571-1630), ma erano noti già da tempo: ad esempio, il primo dei due è raffigurato nel pavimento della basilica di San Marco a Venezia in un intarsio marmoreo del 1420, attribuito a Paolo Uccello.

Quelli che abbiamo appena descritto sono gli unici poliedri regolari aventi come facce dei poligoni stellati, ma non sono gli unici poliedri regolari stellati: se ne possono costruire degli altri, in cui le facce sono poligoni regolari usuali, che però “si intrecciano” tra loro, cioè possono avere in comune dei segmenti che non sono lati delle facce, proprio come i lati di un poligono stellato possono avere in comune dei punti che non sono vertici.
All’inizio del diciannovesimo secolo il fisico matematico Louis Poinsot (1777-1859) trovò due poliedri regolari stellati di questo tipo, il grande dodecaedro e il grande icosaedro, ottenuti rispettivamente con dodici pentagoni e con venti triangoli che si intrecciano a cinque a cinque in ogni vertice, nel senso che vicino a ogni vertice il poliedro ha la forma di una piramide che ha per base un pentagramma. Essi sono raffigurati nel disegno qui sotto (anche in questo caso le aree colorate costituiscono la parte visibile di una delle facce). Pochi anni dopo, il matematico francese Augustin Cauchy (1789-1857) pose la parola fine a questa storia, mostrando che non ci sono altri poliedri regolari stellati.

Tratto dalla scheda I poliedri regolari stellati a cura di Emma Frigerio per la mostra Simmetria, giochi di specchi.