Esiste una grande varietà di fiori i cui petali si distribuiscono simmetricamente attorno al centro. Guardiamo, ad esempio, la pervinca qui accanto e fissiamo l'attenzione su un suo petalo: possiamo passare da questo ad uno degli altri petali ruotando il fiore attorno al suo centro in modo tale che ciascun petalo giunga ad una delle cinque posizioni possibili.

La pervinca ha come simmetrie solo queste cinque rotazioni. 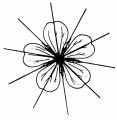L'altro fiore qui a fianco, invece, ha come simmetrie anche le cinque riflessioni rispetto alle cinque rette passanti per il centro e per l'apice di ciascun petalo.

Il tipo di simmetria pentagonale che abbiamo considerato è frequentissimo nel mondo organico: oltre che in molti fiori, lo ritroviamo ad esempio nelle stelle marine e nei ricci di mare. Anche le mele e le pere hanno una simmetria pentagonale: per convincersene, H.S.M. Coxeter suggerisce di tagliare una mela nel modo in cui si taglia un'arancia per spremerla e di osservarne il torsolo. La natura offre molti esempi di forme che hanno una simmetria analoga ma basata su altri numeri. Ad esempio, sei sono le rotazioni che trasformano in se stesso un cristallo di neve (e sei le riflessioni), mentre tre sono le rotazioni (e tre le riflessioni) che mutano in sè una fatta di banana o di zucchino.

Anche nell'arte esistono straordinari esempi di edifici o di decorazioni simmetricamente disposte intorno ad un centro: il Pantheon circolare a Roma, il Battistero ottagonale del duomo di Firenze, alcuni labirinti, i calendari atzechi, i mandala indiani. In particolare, i rosoni delle facciate delle chiese romanico-gotiche hanno dato il nome a tutti i disegni dotati di questo tipo di simemtria, per i quali le simmetrie sono o tutte rotazioni oppure un certo numero di riflessioni più altrettante rotazioni. In effetti non è possibile che un disegno con simmetrie di riflessione ne abbia un numero diverso da quello delle simmetrie di rotazione. Pare che a questa conclusione sia giunto Leonardo da Vinci, quando cercava di determinare tutte le possibili simmetrie di un edificio a pianta centrale.

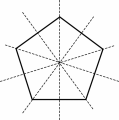
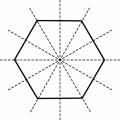Da un punto di vista matematico, i rosoni più semplici sono i poligoni regolari, cioè quei poligoni che hanno i lati e gli angoli uguali. I cristalli di neve, ad esempio, non sono altro che magnifiche elaborazioni di uno stesso tema fondamentale, l'esagono regolare.

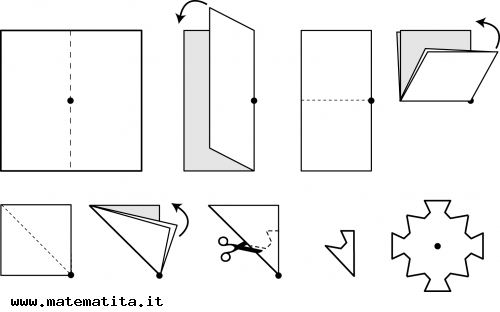
Volete costruire un rosone con la carta? Prendete un foglio, piegatelo più volte con pieghe che passino tutte per un punto, e ritagliatene un profilo: riaprendolo otterrete proprio un rosone. Un rosone costruito in questa maniera ha sempre sia simmetrie di riflessione sia di rotazione. Sapete costruire un rosone di carta con solo simmetrie di rotazione? Non ci sarà bisogno di piegare la carta, ma piuttosto di ...

Tratto dalla scheda I rosoni a cura di Paola Cereda per la mostra Simmetria, giochi di specchi.