Eugenio Beltrami (1835-1900) è stato uno dei più grandi matematici italiani del diciannovesimo secolo e un personaggio di grande rilievo anche sul piano internazionale. Le sue opere spaziano in tutti i campi della matematica e della fisica dell’epoca, ma egli è noto soprattutto per aver individuato nella pseudosfera un primo modello concreto per la geometria non euclidea di Lobatschewsky. Beltrami non si limita ad individuare nella pseudosfera un modello di questa nuova geometria, ma ne costruisce un vero e proprio esemplare in carta. Non si tratta né di un esercizio di tecnica, né di un'esecuzione per scopi espositivi. Beltrami vuole un modello da poter guardare e tenere in mano per poter vedere su di esso i risultati già ottenuti e verificati teoricamente, per individuare nuove proprietà da dimostrare poi nei dettagli e per lasciarsi guidare dall'intuizione verso nuovi risultati. Questa visione spiega perfettamente perché i primi modelli non sono usciti dal suo studio e perché non ne parlò mai in alcuna sua pubblicazione.

I modelli in carta della superficie pseudosferica costruiti tra il 1869 e il 1872 da Eugenio Beltrami sono diversi, ma di essi soltanto uno è arrivato fino a noi ed è quello conservato nell’Istituto di Matematica dell’Università di Pavia.
Si tratta di una superficie flessibile di forma circolare composta da 124 pezzi di carta.

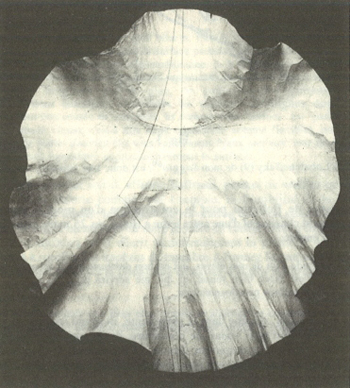
Figura 1: Modello di superficie pseudosferica conservata a Pavia.

Per la sua descrizione seguiamo un articolo di Capelo e Ferrari. Poiché i pezzi di carta altro non sono che porzioni di piano, il modello non risulta in realtà a curvatura costante negativa ma, come scrive Bonola "dà un'idea approssimata della pseudosfera, nella stessa guisa che una poligonale regolare di un numero abbastanza grande di lati da un'idea approssimata di un arco di cerchio".
Ogni frammento di carta approssima un pezzo di pseudosfera delimitato da due paralleli e due meridiani della pseudosfera stessa ed è munito di espansioni tali da permettere l’incollatura a quelli adiacenti.
Per una descrizione più precisa facciamo riferimento al piano ausiliare rappresentato in Figura 2.

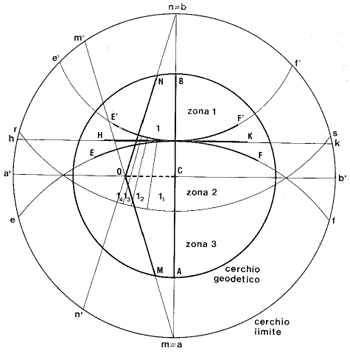
Figura 2: Piano ausiliare per superficie pseudosferica.

Il cerchio esterno è il cerchio limite, cioè l’insieme dei punti all’infinito, mentre il cerchio interno raffigura il cerchio geodetico che racchiude la regione rappresentata nel modello. Tracciamo due diametri geodetici ab e a'b' ortogonali nel centro del cerchio C, le corde geodetiche nn' e mm' parallele al diametro ab, la corda geodetica hk, gli oricicli ef di centro a e e'f' di centro b passanti per l’intersezione tra ab e hk e l’oriciclo rs con centro in b e raggio pari a quello di ef. Nominiamo con le stesse lettere ma maiuscole i punti in cui ogni linea interseca il cerchio geodetico. Gli orocicli e'f' e rs delimitano dunque tre zone del cerchio geodetico, indicate con zona 1, zona 2 e zona 3, in modo che il diametro AB risulta diviso in tre parti di uguale lunghezza.
I “quadrilateri” di carta corrispondono a quelli segnati con e 1₁, 1₂ 1₃, 1₄ e 1, delimitati da due corde geodetiche concorrenti in b e due oricicli di centro b.
A differenza dei “quadrilateri” del piano ausiliario, i “quadrilateri” di carta sono tutti uguali tra loro: i lati rettilinei misurano 0.343 m, il lato curvo più lungo 0.08 m e quello più corto 0.02 m. Fanno eccezione i pezzi più esterni, tagliati in modo che nel complesso il modello abbia una forma circolare, e i 32 “quadrilateri” più laterali della zona 3 che sono stati sostituiti da 16 larghi il doppio. I “quadrilateri” integri sono quindi 20 e tutti compresi nella zona 2.
Le tre zone in cui è diviso il modello si ottengono incollando rispettivamente 14, 42 e 84 pezzi lungo i lati rettilinei. Le tre zone vengono poi incollate lungo i lati curvilinei e, poiché l’arco più corto di ogni “quadrilatero” è un quarto di quello più lungo, a ogni pezzo delle zone 1 e 2 sono attaccati 4 pezzi della zona successiva. In particolare:

• nella zona 1, al 7º “quadrilatero” contando da AB non se ne lega alcuno e al 6º si lega un solo pezzo (questo ad ambo i lati del diametro per la simmetria del modello);
• nella zona 2, al 7º “quadrilatero” da AB si legano due “quadrilateri” normali e uno doppio, agli 8º, 9º e 10º se ne legano due doppi e all’11º un solo pezzo doppio (sempre ad ambo i lati del diametro).

Sul modello in carta realizzato da Beltrami sono visibili alcune linee. Esse corrispondono alle linee più marcate nella figura 2, e più precisamente si tratta di:

• il diametro AB;
• il segmento geodetico OC perpendicolare al diametro AB nel suo punto medio;
• la geodetica ON parallela ad AB che limita, insieme ad AB, un “quadrilatero” della zona 1;
• la geodetica OM parallela ad AB e simmetrica di ON rispetto a OC;
• l’arco d’orociclo E'F' di raggio infinito e di centro b che separa le prime due zone;
• la geodetica HK perpendicolare al diametro AB nel punto in cui esso interseca l’arco E'F';
• l’arco d’orociclo EF simmetrico di E'F' rispetto ad HK (HK è la tangente comune di EF e E'F').

La flessibilità del modello consente di avvolgerlo su se stesso in modo da ottenere le superfici pseudosferiche di tipo iperbolico e parabolico. Non è invece possibile ripiegare il modello in modo da ricreare la superficie pseudosferica di tipo ellittico, a meno di tagliare la superficie.

Figura 3: Superficie pseudosferica di tipo iperbolico.

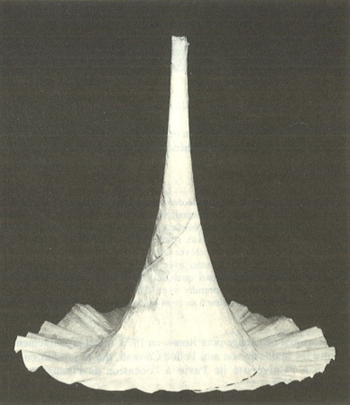
Figura 4: Superficie pseudosferica di tipo parabolico.

Sebbene sia stato costruito nel 1869, il modello materiale della pseudosfera di Beltrami fa la sua prima comparsa pubblica il 16 novembre 1873 durante il discorso di inaugurazione dell'anno accademico 1873-'74 dell'Università di Pavia tenuto da Felice Casorati (1835-1890). Argomento del discorso sono la natura dello spazio e il postulato di Euclide, e dopo aver parlato del concetto gaussiano di curvatura ed esaminato alcuni esempi, Casorati introduce la pseudosfera.
Dopo l'inaugurazione, il modello rimane in possesso di Casorati a Pavia, come testimoniato dai familiari, che lo ricordano in un armadio a vetri della biblioteca del professore. Alla sua morte, avvenuta l'11 settembre 1890, le figlie Eugenia e Bianca ripongono e conservano il modello insieme a tutte le carte e i libri del padre nella villa dell'ingegnere Emilio Franchi Maggi, marito di Bianca. Nel 1902 l'altro genero di Casorati, il professor Gian Antonio Maggi (1856-1937), lo porta a Pisa per mostrarlo ai colleghi dell'università di quella città, dove insegna dal 1895 al 1937. Verso la fine del 1903 il modello torna a Pavia e qui vi rimane fino a che le figlie di Casorati, Eugenia Maggi e Bianca Franchi Maggi, lo donano, come riportato nel verbale della seduta del 21 gennaio 1904 della Facoltà di Matematica e Scienze, all'Istituto Matematico dell'Università di Pavia, dove tutt'ora si trova.

Ma da dove viene questo modello? Molto probabilmente, come si evince comparando le descrizioni, si tratta dello stesso esemplare che Beltrami aveva inviato a Luigi Cremona (1830-1903) il 25 aprile 1869 insieme alla lettera di accompagnamento che è conservata - in copia - con esso all'Università di Pavia e che è stata pubblicata per la prima volta da Capelo e Ferrari nel 1982. A conferma dell'invio a Cremona c'è anche una lettera del 1° maggio 1869 contenuta nel Legato Itala Cremona-Cozzolino presso l'Istituto Mazziniano di Genova, in cui Cremona assicura a Beltrami che "la superficie pseudosferica è arrivata felicemente". Presumibilmente Cremona affida la superficie al collega Casorati nel 1873, anno in cui da Milano si trasferisce a Roma e assume la direzione della Scuola d'Ingegneria.

Nota sulle immagini
Le figure sono tratte dall'articolo A. C. CAPELO, M. FERRARI, La cuffia di Beltrami: storia e descrizione, Bollettino di storia delle scienze matematiche 2 (1982), 233-247.
Le fotografie del modello conservato a Pavia sono presenti anche in L. BOI, L. GIACARDI, R. TAZZIOLI, La Découverte de la Géométrie Non Euclidienne sur la Pseudosphère. Les lettres de Eugenio Beltrami a Jules Hoüel (1868-1881), Blanchard, Paris, 1998.
Altre immagini dello stesso modello sono riportate in R. BONOLA, Il modello di Beltrami di superficie a curvatura costante negativa, Bollettino di bibliografia e storia delle scienze matematiche 1906, 33-38.