una notazione
Un negozio di timbri
Il “negozio di timbri” (orbifold shop) e il “teorema magico” di Conway: il caso dei mosaici
Un’interpretazione suggestiva (dovuta a Conway) dell’analisi della casistica corrispondente ai gruppi dei mosaici è la seguente: immaginiamo che un negozio venda i componenti che abbiamo descritto e che vanno a formare un timbro, cioè punti conici, punti d’angolo, linee specchio, crocette e pallini. Ciascuno di questi componenti ha un costo, e il “listino-prezzi” è il seguente:
- un pallino ο costa 2 Euro
- una crocetta × costa 1 Euro
- un asterisco * costa 1 Euro
- un punto conico n di ordine n costa (n-1)/n Euro
- un punto d’angolo n di ordine n costa (n-1)/2n Euro.
Il “teorema magico” (così lo chiama Conway) afferma allora che un timbro piano (corrispondente a un mosaico) costa esattamente 2 Euro; e che ogni acquisto fatto con 2 Euro produce un timbro piano.
Si può allora con un po’ di pazienza scoprire tutte le possibili combinazioni di pallini, crocette, asterischi, punti conici e punti d’angolo che hanno come costo totale 2 Euro, il che significa che come conseguenza del teorema magico troviamo che sono esattamente 17 i casi che producono un timbro piano, e precisamente:
| ο | 2222 | 333 | 442 | 632 |
| *2222 | *333 | *442 | *632 | |
| 2*22 | 22* | 3*3 | 4*2 | |
| ** | *× | ×× | 22× |
Il “negozio di timbri” (orbifold shop) e il “teorema magico” di Conway: il caso dei fregi
Nel caso dei fregi c’è a disposizione un ulteriore simbolo (∞), che costa 1 Euro se compare prima dell’asterisco *, e 50 centesimi se compare dopo l’asterisco; questa scelta è coerente con il fatto che il limite di (n-1)/n, al tendere di n all’infinito, è 1, mentre il limite di (n-1)/2n, al tendere di n all’infinito, è 1/2. Possiamo quindi immaginarlo come un “centro di ordine infinito” corrispondente non più a una rotazione, bensì a una traslazione.
Il “teorema magico” per i fregi afferma allora che si ottiene un timbro piano corrispondente a un fregio se e solo se il timbro costa esattamente 2 Euro e contiene almeno un simbolo ∞.
Anche in questo caso, con un po’ di pazienza, si arriva a elencare tutte le possibilità, che sono 7:
| ∞ ∞ | 22∞ | ∞× | ∞* | *∞ ∞ | 2*∞ | *22∞ |
Il negozio di timbri (orbifold shop) e il “teorema magico” di Conway: il caso dei gruppi finiti di isometrie dello spazio
Abbiamo detto che la notazione di Conway serve anche per descrivere tutti i possibili tipi di simmetria corrispondenti a gruppi finiti di isometrie dello spazio (e i timbri corrispondenti sono le cosiddette orbifold ellittiche).
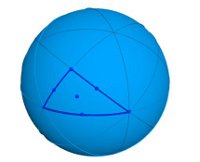
In questo caso, parlando di timbro, ci riferiamo al quoziente rispetto al gruppo (non dell’intero spazio tridimensionale, ma) di una sfera. Per capire da dove spunta questa sfera, cominciamo a considerare un esempio e partiamo da un cubo (che fa le veci del disegno nel caso piano). Il gruppo di simmetria del cubo comprende tutte le isometrie dello spazio che mandano il cubo in sé. Tutte queste trasformazioni fissano un punto, ovvero il centro del cubo, e fissano quindi anche ogni sfera che abbia centro in questo punto.
Sulla sfera che qui vediamo, e che dobbiamo immaginare con centro nel centro del cubo, sono accennate, con colori diversi, le zone che corrispondono alle facce del cubo (come se un cubo azzurro con le sei facce un po’ più chiare o un po’ più scure fosse stato “gonfiato” in una sfera); le linee che si vedono sulla sfera sono archi di cerchio massimo e corrispondono all’intersezione della sfera con i piani di simmetria del cubo; i triangoli sono la proiezione sulla sfera dei 48 (=6×8) triangoli in cui la superficie del cubo è divisa da tutti i piani di simmetria insieme.
Quando parliamo di un timbro in una situazione come quella del gruppo di simmetria del cubo, ci riferiamo proprio al quoziente rispetto al gruppo di una di queste sfere: per ottenere questo timbro, quindi, facciamo ora sulla sfera le stesse operazioni che abbiamo fatto nei primi esempi partendo dal piano: dobbiamo cioè identificare tutti i punti che stanno in una stessa orbita rispetto al gruppo di simmetria del cubo.
Ad esempio, un punto dove convergono 4 cerchi massimi corrisponde al centro di una faccia del cubo, e questi sono tutti “uguali” fra loro (ovvero basta uno di questi punti a rappresentarli tutti nel quoziente), perché comunque si fissino due facce di un cubo riusciamo a trovare un elemento del suo gruppo di simmetria che manda le facce l’una nell’altra; analogamente un punto dove convergono tre cerchi massimi corrisponde ai vertici del cubo, che pure sono tutti uguali fra loro (nella stessa orbita) e quindi danno un solo punto nel quoziente; infine, un punto dove ne convergono due corrisponde ai punti medi degli spigoli del cubo, di nuovo tutti nella stessa orbita. Il quoziente è un triangolo sferico (di angoli 90°, 60° e 45°), e possiamo descrivere questo timbro, nello stesso modo come abbiamo fatto per i timbri piani, con il simbolo di Conway *432.
Se poi calcoliamo il costo totale del timbro, otteniamo 1 + 3/8 + 2/6 + 1/4 = 1 + 23/24 <2.
E questo non è un caso.
In effetti, il “teorema magico” afferma che per ottenere uno di questi timbri (che si dicono ellittici, e sono i quozienti della sfera rispetto a un gruppo finito di isometrie) è necessario che il costo totale sia inferiore a 2 Euro.
La casistica delle possibili maniere di costruire un simbolo di Conway con costo totale minore di 2 Euro comprende 7 casi “singoli” isolati, cioè:
| 332 | 432 | 532 | *332 | *432 | *532 | 3*2 |
e alcune famiglie infinite (che dipendono da un numero n):
| n | nk | n× | n* | *n | *nk | 2*n | 22n |
Nel caso dei timbri piani il fatto che il costo totale fosse 2 Euro era una condizione necessaria, e anche sufficiente all’esistenza del timbro. Nel caso dei timbri ellittici, invece, non è più proprio così, perché ci sono dei casi che vanno esclusi e non danno luogo a un timbro.
I casi da escludere sono 4
| n | *n | nk(quando n#k) | *nk(quando n≠k) |
Restano quindi 7 famiglie infinite:
| nn | 22n | n× | n* | *nn | 2*n | *22n |
Qualcuno avrà forse notato il parallelismo fra queste sette famiglie infinite e i sette gruppi dei fregi; non si tratta solo di osservare che in entrambe le situazioni i casi possibili sono 7, ma, se esaminiamo la lista dei 7 simboli di Conway nell’uno e nell’altro caso, ci accorgiamo che si ottengono proprio l’uno dall’altro sostituendo “n” con “∞”:
| ∞∞ | 22∞ | ∞× | ∞* | *∞∞ | 2*∞ | *22∞ |
Naturalmente non si tratta di una coincidenza e ci sono delle decorazioni che mostrano molto bene il motivo di questo parallelismo. Partendo da un fregio possiamo immaginare di “arrotolarlo” su un cilindro, in modo che quella che era una traslazione, che mandava ogni elemento nel successivo, diventi una rotazione. A volte diamo per scontata, senza neanche renderci conto, questa confusione, parlando tranquillamente di fregi per dei motivi che decorano ad esempio l’abside cilindrica di una chiesa (e quindi non stanno su un piano); li vediamo come fregi, semplicemente perché li immaginiamo “distesi” sulla facciata.
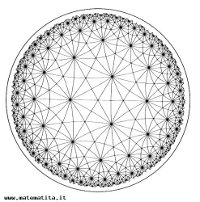
Del tutto diversa (e molto più ricca) è la situazione relativa ai timbri (iperbolici) che corrispondono a un costo maggiore di 2 Euro; in questo caso non possiamo elencarli tutti perché le diverse possibilità sono infinite: qui vediamo un esempio con simbolo di Conway *237 (che in effetti ha costo totale 1 + 1/4 +2/6 + 6/14 = 1+85/84 >2).