Knots at the mirrors
Let us compare a knot with that represented by its mirror image: is it the same knot?
In general, we can not move something onto its mirror image via a rigid motion - just think of a pair of left and right shoes - We will be tempted to say that the two knots are different.
On the other hand, we can perform various motions that move one knot to the other (and conclude that the two knots are the same). For instance, we can wind the string, stretch it a bit as if it were long as much as we want; we can move it in any way as long as we do not untie it. This wide spectrum of operations makes us think that the answer to our original question is positive: after all the two knots "look alike" quite a lot!
Actually, both answers are wrong for all knots. For some knots the answer is "yes" and for some others the answer is "no".
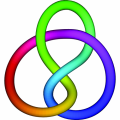
For instance, the figure eight knot is the same as its mirror image . This is easy to verify - just play with a string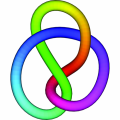 
or follow the links from this image. On the other hand, a right trefoil can not be manipulated until it becomes its mirror image, which is called a left trefoil.
It is not so easy to prove the second claim. In fact, if we are able to manipulate a string till a knot becomes a different one, we are sure that the two knots represent the same one. If we are not able to, how can we say it is indeed impossible? How can we say that we were not able to and that someone else might have succeeded?
Mathematically speaking, to be certain that our claim does not hold, we associate a "mathematical object" with every knot. It could be a number or something even more complicated like, for instance, a polynomial. This object should be concretely and explicitly calculated from a particular position of a knot. For example, we could think of a diagram like one of those in this leaflet or of a string in three-dimensional space. 
The value of this mathematical object may a priori change if we start from a different position of the knot. If, however, we can find some way to associate the knot with the object so that the value of this object does not change with respect to the operations which correspond to the real "manipulation" of the string, we come up with an "invariant" of the knot, i.e., something that depends only on the knot and not on a particular projection or a particular diagram.
If we find an invariant which takes two different values on two different knots, we can be certain that the two knots are really different, i.e., they can not be moved one onto the other.
This is exactly what happens for the right and the left trefoils.
