Le 48 simmetrie del cubo formano una famiglia con interessanti proprietà. Si tratta di una famiglia molto chiusa: il risultato della composizione di due o più elementi della famiglia è sempre un elemento della famiglia.

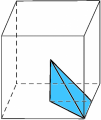La trasformazione identità vi ha un ruolo d’eccezione: è l’elemento neutro della famiglia nel senso che ogni simmetria del cubo composta con l’identità rimane se stessa.

L’ordine con cui si compongono le trasformazioni influisce generalmente sul risultato finale. Nelle figure qui sotto si vede per esempio dove si sposta la piramide di riferimento se prima si riflette il cubo rispetto al piano P e poi lo si ruota di 1/4 di giro attorno alla retta r e dove si sposta se si inverte l’ordine di composizione.

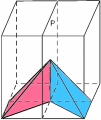
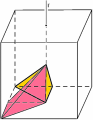
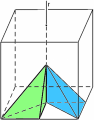
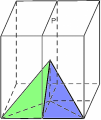
Ogni simmetria del cubo ha una sorella con cui ha un rapporto privilegiato: è la sua inversa, cioè la simmetria che fa ritornare alla posizione di partenza la piramide di riferimento. Se una simmetria viene composta con la sua inversa, indipendentemente dall’ordine, il risultato è l’identità. Per esempio, la rotazione di 1/4 di giro attorno alla retta r ha come inversa la rotazione di 3/4 di giro attorno a r; ogni riflessione rispetto a un piano è l’inversa di se stessa; la composizione, rappresentata nelle figure qui sopra, della riflessione rispetto al piano P e della rotazione di 1/4 di giro attorno alla retta r ha come inversa la composizione della rotazione di 3/4 di giro attorno alla retta r con la riflessione rispetto al piano P (in questo ordine! esattamente come, quando si inverte l’operazione di “infilarsi le calze e poi infilarsi le scarpe”, ci si toglie prima le scarpe e poi le calze e non certo il viceversa!).

Ogni simmetria del cubo composta con se stessa un certo numero di volte dà origine all'identità. Per esempio, la piramide di riferimento torna nella posizione iniziale se eseguiamo quattro volte una rotazione di 3/4 di giro attorno a una retta per i centri di due facce opposte o se compiamo due volte una riflessione rispetto a uno stesso piano di simmetria.
Nel descrivere le caratteristiche della famiglia delle simmetrie del cubo abbiamo dato un esempio di uno dei più importanti concetti matematici: la struttura di gruppo.
Le simmetrie del cubo, con l’operazione data dal fare prima l’una e poi l’altra (la composizione), costituiscono un gruppo; così come è un gruppo anche l’insieme dei numeri interi relativi con l’operazione di somma. Anche questa famiglia è chiusa (la somma di due numeri interi è ancora un numero intero); il numero 0 ha per i numeri il ruolo che la trasformazione identità aveva per la famiglia delle simmetrie del cubo (la somma di un qualunque numero con lo zero è ancora il numero da cui si è partiti); e per ogni numero il fratello, con cui ha un rapporto privilegiato, è il numero di segno opposto (ogni numero, sommato al suo opposto, dà lo zero).

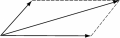Ma la struttura di gruppo si incontra in tantissimi altri contesti, anche molto lontani fra di loro: ad esempio, è un gruppo l’insieme dei vettori del piano, con l’operazione data dalla somma di due vettori secondo la regola del parallelogrammo.

E non solo le simmetrie di un cubo, ma anche le simmetrie di una qualunque figura piana, o un qualunque oggetto solido formano un gruppo con l’operazione di composizione, esattamente come nel caso del cubo.
Se la forma scelta è completamente asimmetrica, il gruppo delle sue simmetrie è il gruppo formato da un unico elemento: la trasformazione identità.

Il gruppo di simmetria della figura piana qui accanto ha sei elementi. (Quali? E qual è l’inverso di ogni elemento?).

I rosoni sono figure piane il cui gruppo di simmetria contiene un numero finito di elementi. Esistono però anche figure il cui gruppo di simmetria contiene infiniti elementi, ad esempio una circonferenza, oppure una retta.

Tratto dalla scheda La famiglia delle simmetrie del cubo a cura di Cristina Vezzani per la mostra Simmetria, giochi di specchi.