Lo studio dei poliedri è spesso collegato al problema della misurazione di alcune grandezze relative ad essi (volume, area delle facce, lunghezza degli spigoli, ampiezza degli angoli diedri, …).
Ma i poliedri possono essere interessanti anche da altri punti di vista: ad esempio una relazione trovata da Eulero nel 1751 lega il numero V dei vertici, quello F delle facce e quello S degli spigoli nel modo seguente:

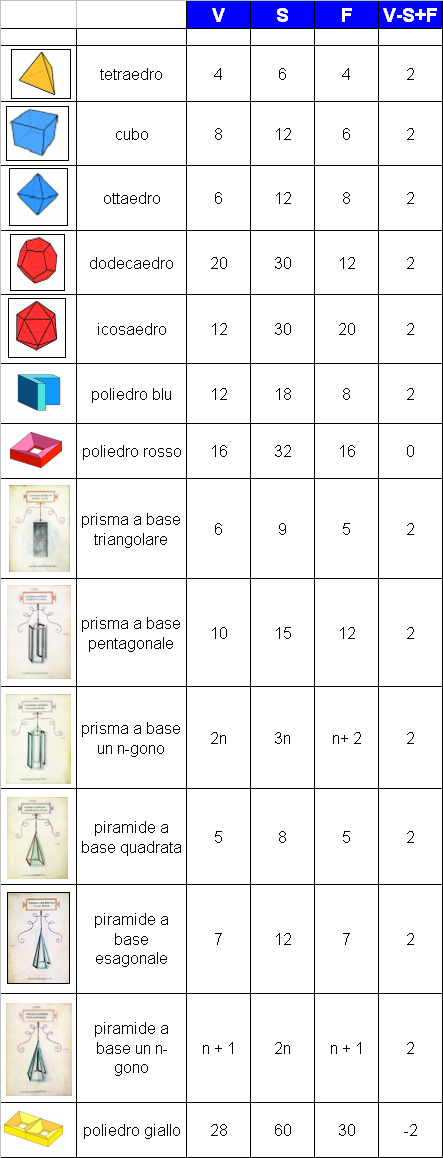
Nella tabella qui sotto si può verificare direttamente la validità della relazione di Eulero nel caso dei cinque poliedri regolari, dei prismi e delle piramidi; la relazione vale anche per altri poliedri (ad esempio per il poliedro blu qui sopra in figura o per i due poliedri viola più sotto), ma non per tutti (ad esempio non vale per i poliedri raffigurati più sotto che abbiamo chiamato poliedro rosso e poliedro giallo); ed è stato in effetti un problema significativo quello di capire esattamente per quali poliedri valesse.

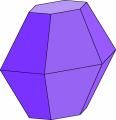
In un primo momento, si pensò che fosse la convessità la caratteristica discriminante dei poliedri che soddisfano la relazione di Eulero, ma poi si comprese che non era così: per esempio, i due poliedri qui accanto sono ottenuti l’uno dall’altro mediante una “strozzatura” a livello della cintura, che evidentemente non cambia i numeri V, S, F; eppure, uno dei due è convesso e l’altro no!

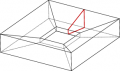
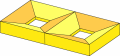
La caratteristica che contraddistingue i poliedri per cui vale la relazione di Eulero è che un qualsiasi taglio continuo e chiuso sulla loro superficie la divide necessariamente in due pezzi: per il poliedro rosso e per il poliedro giallo, invece, si possono trovare tagli continui e chiusi che non dividono la superficie in due pezzi (uno di questi è illustrato in figura): in effetti per questi due poliedri non vale la relazione di Eulero.

Come semplice conseguenza della relazione di Eulero si può ottenere un’altra dimostrazione del fatto che i poliedri regolari sono solo cinque. Un poliedro regolare ha F facce, ciascuna delle quali è un poligono regolare con lo stesso numero h di lati, e in ogni vertice arriva lo stesso numero k di spigoli. Siccome ogni spigolo è comune a due facce, hF è il doppio di S; e siccome ogni spigolo contiene due vertici, kV è il doppio di S. Sostituendo questi dati nella relazione di Eulero, si trova:

da cui, dividendo per 2S, si ottiene:

Tenendo conto del fatto che i valori di h e k sono entrambi maggiori o uguali a 3 (perché ogni faccia ha almeno tre lati e in ogni vertice arrivano almeno tre spigoli), la disuguaglianza

non lascia molte possibilità. Infatti h e k non possono essere entrambi maggiori di 3, perché 1/4 + 1/4 = 1/2, quindi uno dei due è necessariamente uguale a 3; se h=3 si ottiene 1/k > 1/2 - 1/3 = 1/6, e analogalmente per k=3 si ottiene h<6.

Le sole possibilità per h e k sono quindi:

• h=k=3 (tetraedro: facce triangolari, tre in ogni vertice)
• h=3 e k=4 (ottaedro: facce triangolari, quattro in ogni vertice)
• h=3 e k=5 (icosaedro: facce triangolari, cinque in ogni vertice)
• h=4 e k=3 (cubo: facce quadrate, tre in ogni vertice)
• h=5 e k=3 (dodecaedro: facce pentagonali, tre in ogni vertice)

Dai valori di h e k si possono poi ricavare i valori di S, V, F. Per esempio, sostituendo h=4 e k=3 (corrispondenti al caso del cubo) in 1/h + 1/k = 1/S + 1/2 si trova 1/S = 1/4 + 1/3 - 1/2 = 1/12, cioè S = 12 e quindi F = 24/4 = 6, V = 24/3 = 8.
Vale la pena notare che questa dimostrazione che i poliedri regolari sono solo cinque non usa alcun fatto di tipo metrico (lunghezza degli spigoli, ampiezza degli angoli…).

Tratto dalla scheda La relazione di Eulero a cura di Alessia Cazzola per la mostra Simmetria, giochi di specchi.