In ogni rappresentazione dell'ipercubo si dovrebbe “vedere” ognuna delle otto facce cubiche dell'ipercubo. Questo è chiaro per lo sviluppo, ma nel caso del diagramma di Schlegel e della proiezione? Dove sono gli otto cubi?

Nel diagramma di Schlegel si può osservare la rappresentazione di sette
delle otto facce cubiche dell'ipercubo. Un cubo piccolo all'interno e altri sei cubi deformati che si incollano faccia contro faccia e formano il cubo grande esterno. Dove è l'ottavo cubo? L'ottavo cubo ha come facce le facce del cubo grande; ma visto che l'interno del cubo grande è già “occupato” dagli altri sette cubi, possiamo pensare che l'interno dell'ottavo cubo sia l'esterno del cubo grande, che è uno spazio non limitato!

Questa osservazione nasce dal fatto che ragioniamo nello spazio tridimensionale. Il caso del diagramma di Schlegel del cubo nel piano può aiutarci a comprendere meglio il caso dell'ipercubo.

Anche nel diagramma di Schlegel del cubo notiamo che manca una faccia, che è quella delimitata dal quadrato grande. Ma in realtà questa è una proiezione bidimensionale; in effetti dobbiamo pensare che le cinque altre facce vivono in “primo piano” (come in rilievo) rispetto alla sesta faccia, delimitata appunto dai lati del quadrato grande.

Allo stesso modo, nel diagramma dell'ipercubo i sette cubi che appaiono all'interno sono da immaginare come in “primo piano” rispetto alla faccia cubica delimitata dal cubo grande; questa prospettiva appare meno evidente che nel caso del cubo in quanto stiamo mentalmente aggiungendo una dimensione al nostro spazio tridimensionale per mettere in rilievo quello che appare all'interno del cubo grande; ma questo significa “vedere” in uno spazio a quattro dimensioni...
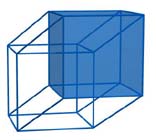
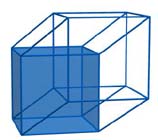
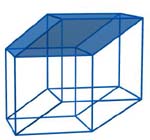
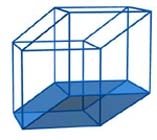
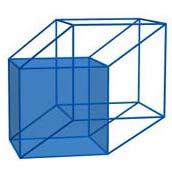
Nel caso della proiezione dell'ipercubo due cubi sono evidenti, ma dove sono gli altri? Prendiamo in considerazione una proiezione del cubo su un piano;le proiezioni delle sei facce “si accavallano” tra di loro; così pure nel caso della proiezione dell'ipercubo le proiezione delle otto facce cubiche si intersecano tra di loro: per osservarle, consideriamo le “basi” di questi due cubi;

si può facilmente osservare che sono le basi anche di due altri solidi (primo, secondo) con otto vertici e dodici spigoli, che sono la proiezione di altre due facce cubiche. Mancano quindi all'appello ancora quattro cubi; lasciamo a voi il compito di scoprire dove si “nascondono”...

A cura di Paolo Bellingeri per la mostra Un tuffo nella quarta dimensione.