Sono molti gli oggetti dotati di simmetria bilaterale: armadi, lampadari, cartelli stradali, bandiere, strumenti musicali,la maggior parte dei nostri abiti (ma non i guanti, e non le scarpe...). E moltissimi anche gli animali, e i tipi di foglie; lo stesso corpo umano, nella sua esteriorità, è sostanzialmente dotato di simmetria bilaterale (diverso sarebbe il discorso se pensassimo anche agli organi interni).

Ma che cosa significano le frasi "questa farfalla ha una simmetria bilaterale" oppure "questa farfalla ha un piano di simmetria"?
Se immaginiamo di tagliare qualcosa a metà lungo un suo piano di simmetria e di collocare uno specchio nella posizione di questo piano, allora l'immagine riflessa insieme all'oggetto dimezzato ricostruiscono l'oggetto iniziale.

In pratica è un po' difficile - e/o dispendioso - tagliare a metà una forchetta, per non parlare di una farfalla o di un essere umano (anche se la fantasia di Italo Calvino ci ha provato con il visconte dimezzato...).
E' più facile fare un esperimento analogo nel caso di una figura piana, per la quale la simmetria non è più rispetto ad un piano, ma rispetto a una retta (asse di simmetria). Possiamo utilizzare uno specchio per controllare se una retta è o non è asse di simmetria per una certa figura, collocandolo lungo la retta in questione, perpendicolarmente al piano della figura: se la retta è un asse di simmetria,
come nella figura qui accanto, allora la mezza figura insieme all'immagine riflessa ricostruiscono una figura identica a quella da cui siamo partiti; altrimenti questo non accade. E, come si vede dalle figure qui sotto, ciò può benissimo non accadere anche se la retta in questione divide la figura in due parti uguali.

Ma che cosa succede utilizzando due specchi? Supponiamo, ad esempio, di inserire una p fra due specchi paralleli: si vede allora una serie di immagini che si ripetono lungo una striscia, alternando immagini della p con immagini della q.

Se si fa prima una riflessione, ripetto ad una retta, e poi un'altra riflessione, rispetto ad un'altra retta, parallela alla prima, l'effetto che si ottiene equivale a quello di una traslazione, in una direzione perpendicolare alle due rette, di una distanza doppia della distanza tra le due rette.

Una riflessione scambia la destra con la sinistra: infatti l'immagine allo specchio di una p, che ha la zampa a sinistra, è una q, con la zampa a destra. Una traslazione, invece, equivale a due riflessioni e quindi... la zampa della p si ritrova al suo posto; così come la coda del gatto nella figura qui sotto.

E se gli assi non sono rette parallele, ma sono due rette incidenti?


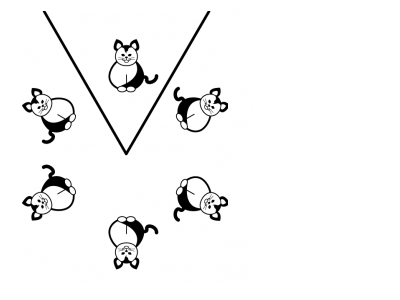
Mettendo un oggetto tra due specchi incidenti (per esempio, come qui in figura, un gatto con la coda a destra), si vedono ancora un po' di immagini dell'oggetto, e fra di esse si alternano quelle che hanno la coda a sinistra e quelle che l'hanno a destra; le immagini però non si dispongono più lungo una striscia, ma piuttosto intorno ad un centro. In effetti, se si fa prima una riflessione rispetto ad una retta, e poi un'altra riflessione rispetto ad un'altra retta, che ha in comune con la prima un punto, l'effetto che si ottiene equivale a quello di una rotazione intorno a questo punto, di un angolo doppio dell'angolo tra le due rette.

Quante immagini si vedono?
Se l'angolo fra i due specchi è un sottomultiplo dell'angolo piatto, come nelle figura qui sopra (in cui l'angolo è di 60 gradi, che è 1/3 dell'angolo piatto), allora l'intero angolo giro è diviso dagli specchi - reali e virtuali - in un numero pari di angoli (sei qui in figura) ciascuno dei quali contiene un'immagine: metà (tre qui in figura) contengono un'immagine che si ottiene dall'oggetto iniziale con una rotazione (e quindi il gatto con la coda a destra), mentre gli altri si ottengoo dall'oggetto iniziale con una riflessione (e quindi il gatto con la coda a sinistra).
Che cosa succede se l'angolo non è un sottomultiplo dell'angolo piatto?

Tratto dalla scheda Le riflessioni a cura di Paola Cereda per la mostra Simmetria, giochi di specchi.