Quanto e come è simmetrico un cubo? Basta poco a convincersi che è più simmetrico di un parallelepipedo: se quattro persone, sedute intorno a un tavolo quadrato, osservano un cubo appoggiato sul tavolo, vedono tutte la stessa cosa; se invece sul tavolo c’è un parallelepipedo (con le tre dimensioni diverse fra loro), solo le due coppie di persone che stanno di fronte vedono la stessa cosa.

E' possibile far vedere che le differenti simmetrie del cubo sono 48. Per un cubo sono nove i piani di simmetria, cioè i piani che lo dividono in due parti, l’una immagine speculare dell’altra.

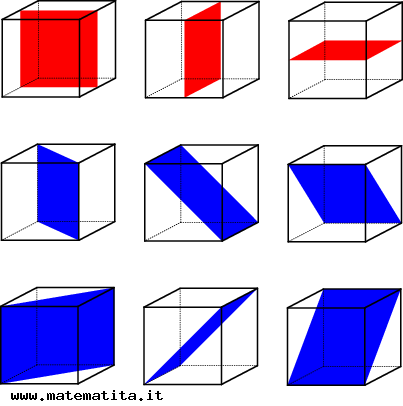
Questi piani passano tutti per il centro del cubo e, se vengono considerati tutti insieme, dividono la superficie del cubo in 48 triangoli uguali e il cubo stesso in 48 piramidi uguali che per base hanno i 48 triangoli, e per vertice il centro del cubo.

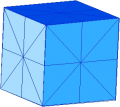
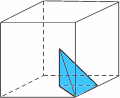
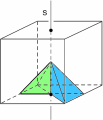
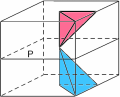
Scelta come riferimento una di queste 48 piramidi, ogni simmetria del cubo la sposta in una delle 48 posizioni possibili, compresa quella da cui era partita (in quest’ultimo caso è come se tutto il cubo fosse rimasto fermo e la simmetria viene chiamata trasformazione identità). Per esempio nelle figure qui sotto vediamo dove si sposta la piramide dopo una rotazione di mezzo giro attorno alla retta s o dopo una riflessione rispetto al piano P.
Ruotando il cubo di un giro completo attorno alla retta s, o riflettendolo due volte rispetto a P, si ha invece l’identità: la piramide torna nella posizione iniziale.

Per capire come sono fatte le 48 simmetrie del cubo, possiamo cominciare a descrivere esplicitamente le rotazioni, individuando innanzitutto quali sono i possibili assi di rotazione, cioè le rette attorno alle quali far ruotare il cubo in modo che torni in se stesso. Queste rette possono essere di tre tipi:

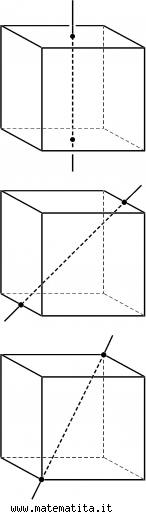
• Rette che passano per i centri di due facce opposte. Le rotazioni intorno a queste rette di 1/4, 1/2 e 3/4 di giro sono simmetrie del cubo, ma lo è anche la rotazione di un giro completo, che corrisponde all’identità. Nel cubo ci sono tre distinte rette di questo tipo e quindi abbiamo individuato dieci simmetrie.

• Rette passanti per i punti medi di due spigoli opposti. Le rotazioni attorno a queste rette che fissano il cubo (a parte l’identità, che abbiamo già contato) sono solo quelle di mezzo giro; le rette di questo tipo sono sei e quindi abbiamo trovato altre sei simmetrie del cubo.

• Rette passanti per due vertici opposti. Il cubo in questo ultimo caso può essere ruotato di 1/3 o 2/3 di giro (a parte l'identità, che abbiamo già contato); ci sono quattro coppie di vertici opposti e quindi altre otto simmetrie di rotazione.

Ci sono dunque in totale 24 differenti simmetrie di rotazione.

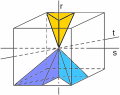
Tra le rimanenti 24 ci sono le nove simmetrie di riflessione rispetto ai nove piani da cui siamo partiti, e altre 15 che sono un po’ più complicate da descrivere esplicitamente, ma che si possono facilmente vedere come trasformazioni composte, cioè ottenute facendo seguire una all’altra due trasformazioni, e considerando poi la trasformazione complessiva.
Se componiamo due delle 24 rotazioni, non scopriamo nessuna nuova simmetria, perché il risultato è ancora una rotazione (anche se questo non sempre è facile da visualizzare: per esempio si vede subito che componendo due rotazioni attorno alla retta r, la prima di 1/4 di giro e la seconda di mezzo giro, si ottiene la rotazione di 3/4 di giro, sempre intorno alla stessa retta; mentre è più complicato vedere che componendo una rotazione di 1/4 di giro attorno alla retta r con una rotazione di mezzo giro attorno alla retta s, si ottiene una rotazione di mezzo giro intorno alla retta t).

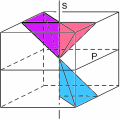
Se invece componiamo una delle nove riflessioni con ognuna delle 24 rotazioni, troviamo tutte le 24 rimanenti simmetrie del cubo che non sono rotazioni: quelle cercate (tra le quali ci saranno anche le nove riflessioni). Nella figura si vede per esempio dove finisce la piramide di riferimento componendo la riflessione rispetto al piano P con una rotazione di mezzo giro attorno alla retta s.

Tratto dalla scheda Le simmetrie del cubo a cura di Cristina Vezzani per la mostra Simmetria, giochi di specchi.