Se voleste rifare il pavimento della cucina dovreste acquistare delle piastrelle. Potreste acquistarne solo di quadrate, tutte dello stesso lato. Magari ve ne servirebbero molte (cento, mille…), a seconda della superficie da ricoprire e della dimensione dei quadrati, ma comunque ve ne servirebbe un numero finito.

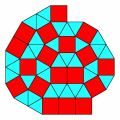Un problema seccante potrebbe essere che, secondo la forma della stanza, potreste essere obbligati a tagliare alcune piastrelle, per colmare quegli spazi, vicini alle pareti, che non potrebbero essere riempiti con piastrelle intere. Per esempio, se voleste un pavimento un po’ diverso dal solito, fatto con piastrelle di due tipi (non solo quadrati, ma anche triangoli equilateri dello stesso lato, come nei disegni qui a fianco) e se la vostra cucina fosse perfettamente quadrata (di una larghezza qualsiasi), beh, allora dovreste munirvi di uno strumento per tagliare le piastrelle!
Tuttavia, se siete romantici e la vostra cucina “non ha più pareti”, allora potete piastrellarla senza ricorrere ad un tagliapiastrelle… dovete solo procurarvi “infinite” copie di tali piastrelle quadrate e triangolari, fare un po’ di attenzione e avere molta, molta pazienza…

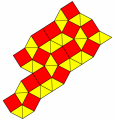In matematica ci si occupa di questi pavimenti infiniti e si chiama tassellazione del piano un ricoprimento del piano fatto con delle “piastrelle” che non si sovrappongono e non lasciano buchi (niente tagliapiastrelle, insomma). Esempi di tassellazioni sono quelli che si vedono nelle camere degli specchi della mostra Simmetria, giochi di specchi. Se la tassellazione è costruita a partire da un numero finito di tipi di piastrelle (come quelle delle figure qui accanto che sono costruite solo con quadrati e triangoli equilateri), allora dovranno esserci infinite copie per almeno un tipo di piastrella, altrimenti si riuscirebbe a coprire solo una regione del piano, magari molto vasta, ma (di area) finita.

Possiamo quindi pensare a un problema di questo tipo: se abbiamo delle piastrelle, tante quante ne vogliamo, ma solo di alcuni tipi prefissati, quali sono le tassellazioni che possiamo ottenere con queste piastrelle? Ce ne sarà almeno una? Ce ne saranno tante? Quante? Fatte in che modo?

Sembra un problema piuttosto semplice, e invece non lo è affatto, neppure se pensiamo soltanto a tassellazioni fatte con un solo tipo di piastrella. Ci sono poligoni che tassellano il piano (per esempio un quadrato) e poligoni che non lo tassellano affatto (per esempio un pentagono regolare). Si può costruire un pavimento infinito con piastrelle soltanto quadrate, ma non si può costruire una tassellazione fatta di soli pentagoni regolari.

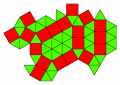
Se disegnate un triangolo qualsiasi e fate un po' di prove, potete rendervi conto che esistono delle tassellazioni del piano che sono costituite da infinite copie di tale triangolo. Questo dato "sperimentale" ("QUESTO triangolo che ho disegnato può tassellare il piano") può essere abbastanza facilmente tramutato in una affermazione di carattere generale ("OGNI triangolo tassella il piano"); e la stessa cosa succede se si parte da un qualsiasi quadrilatero (vedi ad esempio le figure qui accanto).

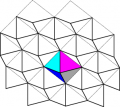Invece, un poligono convesso con almeno sette lati non può mai tassellare il piano; quest'ultima asserzione però non è evidente e la sua dimostrazione è complessa.
Se vi interessate solo ai poligoni convessi, vi rimangono dunque da esaminare due casi dubbi: i pentagoni e gli esagoni.
Il fatto curioso è che, mentre si può sempre decidere, a partire da una piastrella esagonale, se questa tassella il piano oppure no, la classificazione dei pentagoni che tassellano il piano è un problema tuttora aperto.

Fra i pentagoni che non tassellano il piano vi è quello colorato nella figura qui sotto. Attorno ad esso, nella stessa figura, abbiamo costruito una "corona" di pentagoni che hanno in comune con quello di partenza un lato, una porzione di lato o un vertice. Questo insieme di pentagoni si chiama la 1-corona del pentagono giallo.
Qualche volta (ma non è questo il caso in figura!) si può costruire, a partire dai pentagoni della 1-corona, una seconda corona (la 2-corona)e poi ancora una terza e così via.
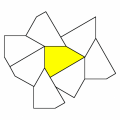
Ad ogni poligono P si può così associare un numero che rappresenta il numero massimo di corone che riusciamo a costruire intorno ad esso: tale numero si chiama numero di Heesch di P. Questo numero è infinito per i poligoni che tassellano il piano ed è uno per il pentagono in figura; in generale però non si sa se, dato un numero arbitrario, diciamo 47, esista o meno un poligono P con numero di Heesch 47. Addirittura fino a poco tempo fa non si conoscevano poligoni con numero di Heesch finito e maggiore di tre, e solo molto recentemente sono stati trovati esempi di un poligono con numero di Heesch quattro, e di uno con numero di Heesch cinque.

Tratto dalla scheda Le tassellazioni a cura di Paolo Bellingeri per la mostra Simmetria, giochi di specchi.