Confrontiamo un nodo con quello rappresentato dalla sua immagine speculare: sono lo stesso nodo?

In generale non riusciamo con un movimento rigido a portare qualcosa a sovrapporsi con la sua immagine speculare (basta pensare alle due scarpe destra e sinistra…), e quindi saremmo tentati di dire che anche i nodi sono diversi.

Peraltro, in questa situazione, i movimenti che possiamo compiere per portare un nodo nella stessa posizione di un altro (e concludere che i due nodi sono lo stesso nodo) ci lasciano una libertà molto più ampia: possiamo avvolgere la corda, stiracchiarla supponendola lunga a nostro piacimento, possiamo spostarla come vogliamo, pur di non “aprirla”. E questo fatto può farci pensare che la risposta alla domanda iniziale sia sempre e comunque un sì: dopotutto i due nodi “si assomigliano” molto.

In realtà ne la prima ne la seconda risposta “vanno bene” per tutti i nodi: ci sono alcuni nodi per i quali la risposta è sì e altri per i quali la risposta è no.
Ad esempio, il nodo "a otto" è la stessa cosa della sua immagine speculare, e questo è facile da verificare (basta giocare con la corda! 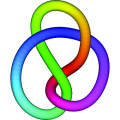oppure seguire i
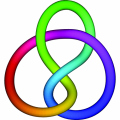
link ipertestuali a partire ad esempio da questa immagine); invece un nodo trifoglio destro non può essere manipolato fino a diventare la sua immagine speculare che chiamiamo un nodo trifoglio sinistro.

Questa seconda affermazione, però, non è facile da giustificare: in effetti, se, manipolando una corda, riusciamo a portare un nodo nella posizione di un altro, siamo sicuri che i due nodi rappresentano in realtà lo stesso nodo. Ma se non ci riusciamo, come facciamo a sapere che la cosa è davvero impossibile e che non si tratta invece del fatto che noi non siamo stati capaci di farlo e che magari un altro ce l’avrebbe fatta? In matematica, per ottenere la certezza di tale impossibilità, si può procedere in questa maniera: si associa ad ogni nodo un qualche “oggetto matematico” (potrebbe essere un numero, o anche qualche cosa di più complicato, come per esempio un polinomio) che sia direttamente ed esplicitamente calcolabile a partire da una particolare posizione del nodo (possiamo pensare ad un disegno, come uno di quelli di questa scheda, o anche al dato concreto di una corda nello spazio tridimensionale). A priori, il valore di questo oggetto matematico potrà cambiare se si parte da una diversa posizione del nodo; se però troviamo una maniera di compiere questa associazione in modo che il valore di tale oggetto non cambi rispetto alle operazioni che corrispondono alla effettiva “manipolazione della corda”, allora abbiamo a disposizione un “invariante” del nodo, ossia qualcosa che dipende proprio solo dal nodo stesso, e non da una sua particolare proiezione o da un suo particolare disegno.
E se poi si trova un invariante che assume due valori diversi per due nodi, possiamo affermare con certezza che i due nodi in questione sono effettivamente differenti, cioè che non esiste una manipolazione che li porti l’uno nell’altro.
E questo è per l’appunto ciò che si è trovato per il nodo trifoglio destro e sinistro.