Paths with no crossing

Let us suppose to connect the three main railway stations in Milan (Centrale, Nord and Garibaldi) with the Cathedral, the stadium and the Linate airport via a system of fast trains. It is therefore necessary that the connecting paths do not cross. Is it possible?

This is a revised version in the Milan area of a classical topological problem, which can be worded in this way. Fix three points (in the figure three coloured dots; in our example the cathedral, the stadium and the airport). You must connect each black dot with each of the coloured dots so that the paths do not cross.

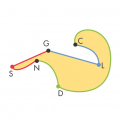This is a topological problem because it is easy to realize that the distance between the dots does not matter as well as where they lie. Actually, our original problem is not realistic because we should have trains for which the manufacturing cost does not depend on the length of the paths and the travelling times are not length-dependent!
You may start drawing the possible paths from a black dot. You may also get to draw all the paths except one. After that, you are done. You can not connect the Nord Station with Linate without crossing the other paths. This does not depend on a possible mistake in drawing the first paths: it is actually impossible!
To realize that the problem is in fact impossible, you may think of the circuit (sketched in the picture) with six paths: Central Station - Cathedral - Nord Station - Stadium - Garibaldi Station - Linate - Central Station.
However you draw the paths, this circuit is a closed curve without crossings (for the paths do not cross). Such a curve separates the plane in two regions: an internal part and an external one. Thus, any one of the three paths we have to add is completely in the internal region or completely in the external one.

It is easy to see it is not possible to solve the problem. If, for instance, one of the three paths to be added is in the internal region of the circuit, the second path should be in the external region; so the third path is blocked both inside and outside.

The crucial point that makes the problem impossible to solve is that any closed curve without self-intersections divides the plane into two regions, an "inside" and an "outside". This statement is not surprising. Yet, it is the typical example of a theorem (the Jordan curve theorem) which has a very intuitive, and apparently trivial, statement, but it is highly non-trivial to prove. Indeed, it is necessary to apply very sophisticated techniques or, if you do not want to use them, you need very involved arguments. To realize that this theorem is non-trivial, you may observe that the same statement is not true on a torus, i.e., a doughnut, nor on a Moebius strip. This is the surface which is obtained from a rectangle if you glue the two short opposite edges after you give a half twist to the rectangle. Notice that the rectangle should be quite long and narrow if you really want to make a Moebius strip.
On these surfaces it is possible to trace closed non-intersecting curves that do not divide the surface into two regions! We expect to solve our original problem, and in fact this is the case, as you can see from our models (a torus and a Moebius strip)from the exhibition matemilano.

Let us go back to our problem. An alternative - here you see another map - ) makes you connect three black dots with three coloured dots via nine paths, which do not cross, on a map where you can go out from one edge of the rectangle and come back from the opposite edge following some rules.
This situation corresponds to ask the question on another surface, that is to say, on the surface which is obtained by gluing the edges following the rules which settle how to go back from an edge after you go out from the opposite edge - see the virtual leaflet fantamilano. The problem can be solved in the two cases above. In fact, they correspond to the torus and to the Moebius strip respectively.