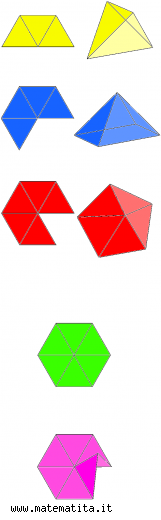
i cinque poliedri regolari
Perché solo cinque?
Per costruire un poliedro regolare, dobbiamo prendere tante copie dello stesso poligono regolare e unirle lungo gli spigoli (in modo che ci sia sempre lo stesso numero di copie intorno a un vertice). Quante sono le possibilità?
Incominciamo a cercare i poliedri regolari con facce triangolari. Se mettiamo insieme tre triangoli equilateri intorno a uno stesso vertice, otteniamo il tetraedro; se ne mettiamo quattro, ritroviamo l’ottaedro e se ne mettiamo cinque, generiamo l’icosaedro. Sei triangoli equilateri che concorrono in un vertice sono troppi perché stanno su uno stesso piano, mentre se se ne mettono insieme sette o più si ottiene necessariamente un solido concavo; quindi non ci possono essere altri poliedri regolari con facce triangolari. Passiamo ai quadrati. Possiamo costruire soltanto il cubo mettendo insieme tre quadrati in ogni vertice, dal momento che quattro quadrati sono già troppi perché stanno su uno stesso piano. Con i pentagoni regolari possiamo costruire solo il dodecaedro, prendendone tre per vertice, perché il pentagono regolare ha gli angoli così grandi che quattro sono troppi.
Non ci sono altre possibilità di costruire poliedri regolari perché con poligoni regolari aventi più di cinque lati, anche solo tre copie sono troppe perché le si possa unire intorno a un vertice del poliedro: tre esagoni regolari stanno su uno stesso piano e l’ampiezza degli angoli in gioco aumenta con il crescere del numero dei lati.Poliedri che “si assomigliano”
Da quanto detto finora potrebbe sembrare che i poliedri regolari siano soltanto cinque perché è “troppo” forte il vincolo che in ogni vertice si incontri lo stesso numero di poligoni regolari uguali fra di loro. In realtà non è tanto la regolarità dei poligoni o l’uguaglianza tra di loro a vincolare la situazione, quanto la regolarità della “struttura” del poliedro: vediamo in che senso.

Se si confronta un parallelepipedo qualsiasi con i cinque poliedri regolari, salta subito all’occhio che esso assomiglia a un cubo più che a uno qualunque degli altri. Il parallelepipedo e il cubo hanno la stessa struttura: in tutti e due le facce sono poligoni a quattro lati e in ogni vertice arrivano tre spigoli.
Allo stesso modo una qualsiasi piramide a base triangolare assomiglia di più al tetraedro, che non ad un altro dei poliedri regolari, perché ha la sua stessa struttura: facce con tre lati e tre spigoli per ogni vertice.
Invece una piramide a base non triangolare, o un tronco di piramide a base non rettangolare, o anche il pallone da calcio, sono essenzialmente diversi dai cinque poliedri regolari: in un poliedro regolare tutte le facce hanno lo stesso numero h di lati e in ogni vertice arriva lo stesso numero k di spigoli, mentre in questi solidi ciò non accade.
Un poliedro ha una “struttura regolare” se tutte le sue facce hanno lo stesso numero h di lati e in ogni suo vertice arriva lo stesso numero k di spigoli: i cinque poliedri regolari, i parallelepipedi a base rettangolare, le piramidi a base triangolare sono esempi di poliedri con struttura regolare. Un risultato matematico profondo e ricco di significati e sviluppi afferma che per un poliedro con struttura regolare ci sono solo cinque possibilità:
- h=k=3 (come per il tetraedro),
- h=4 e k=3 (come per il cubo),
- h=3 e k=4 (come per l’ottaedro),
- h=5 e k=3 (come per il dodecaedro),
- h=3 e k=5 (come per l’icosaedro).

| Tratto dalla scheda Perché solo 5? a cura di Cristina Vezzani per la mostra Simmetria, giochi di specchi. |