Supponiamo di voler collegare le tre stazioni principali di Milano (Centrale, Nord e Garibaldi) con il Duomo, lo stadio e l'aeroporto di Linate mediante un sistema di metropolitana superficiale veloce, per la quale è necessario che i percorsi non si incrocino. È possibile?

Questa è una versione in contesto “milanese” di un problema topologico classico, che si può schematizzare così: si fissano tre punti (in figura indicati con pallini neri; nel nostro esempio le tre stazioni) e tre altri punti (in figura indicati con pallini colorati; nel nostro esempio il Duomo, lo stadio e Linate) e si cerca di collegare ciascuno dei pallini neri con ciascuno dei pallini colorati, in modo che i percorsi non si incrocino. (In realtà il problema "milanese" avrebbe qualcosa di poco reale, perché dovremmo ipotizzare una metropolitana i cui costi di fabbricazione non dipendano dalla lunghezza dei percorsi e i tempi di percorrenza non siano significativamente diversi al variare delle lunghezze!).

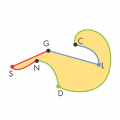Si tratta di un problema topologico, perché è semplice osservare che non ha alcuna importanza come siano disposti i sei pallini nè quanto siano distanti tra loro.
Si può cominciare a tracciare i possibili percorsi che escono da un pallino nero; si può anche arrivare a tracciare tutti i percorsi tranne uno; ma poi non si può fare altro: non si può collegare la Stazione Nord con Linate senza incrociare gli altri percorsi. E questo non dipende dal fatto che abbiamo sbagliato a tracciare i primi: il problema è proprio impossibile!
Per rendersi conto di questa impossibilità, si può pensare al circuito (schematizzato in figura) formato dai sei percorsi: Stazione Centrale - Duomo - Stazione Nord - Stadio - Stazione Garibaldi -Linate - Stazione Centrale.
Comunque siano stati costruiti i percorsi, questo tragitto costituisce una curva chiusa e senza incroci (perché i percorsi non possono attraversarsi tra loro) e una tale curva divide il piano in due parti: una parte "interna" e una "esterna". Quindi, ciascuno dei tre ulteriori percorsi che dobbiamo aggiungere, per evitare di incrociare i primi sei, dovrà stare o tutto all'interno o tutto all'esterno rispetto a questa curva.

È facile vedere allora che non è possibile portare a termine il compito: se per esempio uno dei tre percorsi da aggiungere viene disegnato all'interno del circuito, il secondo dovrà necessariamente passare per l'esterno e il terzo si troverà bloccato sia all'interno che all'esterno.

Il punto cruciale che “blocca” la soluzione è quindi il fatto che ogni curva chiusa e senza incroci divide il piano in due regioni, un "dentro" e un "fuori". Questa affermazione non stupisce: eppure è il tipico esempio di un teorema (il teorema della curva di Jordan) che, pur avendo un enunciato estremamente intuitivo, e all'apparenza banale, non è affatto facile da dimostrare: è necessario infatti usare strumenti molto sofisticati, oppure, se rinunciamo ad essi, costruire un'argomentazione assai laboriosa. Per rendersi conto della non banalità di questo enunciato è utile pensare al fatto che la stessa affermazione non è più vera su un toro (che è una superficie a forma di ciambella), nè su un nastro di Moebius (che è la superficie ottenuta per esempio da un rettangolo - abbastanza lungo e stretto, se vogliamo realizzarlo fisicamente da un pezzo di carta - attaccando insieme i due lati opposti corti dopo aver dato al rettangolo una mezza torsione).
Su queste superfici è possibile trovare curve chiuse non intrecciate che non dividono la superficie in due regioni! E ci aspettiamo allora che su di esse si possa risolvere il problema, come si può vedere anche nei modelli (un toro e un nastro di Moebius) della mostra matemilano.

Torniamo al problema iniziale: una sua variante (questa ne è un'altra forma) prevede che (dovendo ancora unire i tre pallini neri con i tre pallini colorati, disegnati ad esempio su un foglio di carta, con nove percorsi che non si incrocino) sia possibile però uscire dalla cartina per un lato del rettangolo e rientrare, con certe regole, dal lato opposto.
Questa situazione corrisponde a porsi il problema non più sul rettangolo, ma su un'altra superficie, ovvero sulla superficie ottenuta attaccando insieme i lati secondo le regole che fissano come si rientra da un lato dopo essere usciti dal lato opposto (vedi anche l'approfondimento Fantamilano). E quindi nei due casi qui illustrati il problema ha soluzione, dato che le regole corrispondono proprio a ottenere il toro in un caso e il nastro di Moebius nell'altro.

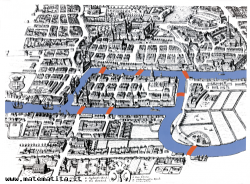
Su queste tre piantine (la prima, la seconda, la terza) sono indicati, con vari colori, alcuni itinerari turistici per Milano.

Il problema posto nei tre casi è lo stesso: è possibile, partendo da un punto qualsiasi di un itinerario, percorrerne tutti i tratti senza staccare la matita dal foglio e senza ripassare mai su strade già percorse?
Dopo qualche tentativo di soluzione, sembra naturale rispondere che alcune volte è possibile e altre no. Perché?

È abbastanza evidente che i vincoli che possono portare all'impossibilità non sono legati alla lunghezza o alla disposizione dei tratti di strada, ma piuttosto a quanti sono, e di che tipo, i punti in cui si incontrano diverse strade (se in un dato incrocio si incontrano tre strade, oppure quattro, o cinque, o sei, o anche di più). Ogni volta che arriviamo ad un incrocio, dobbiamo poi uscirne percorrendo un tratto di strada diverso da quello di entrata. Perciò, se vogliamo finire la passeggiata nello stesso punto dal quale siamo partiti, in ogni incrocio devono confluire un numero pari di strade (nel seguito, chiameremo questi punti incroci pari). Se invece punto di arrivo e di partenza sono diversi, allora in questi due punti devono confluire un numero dispari di strade: dal punto di partenza dovremo uscire una prima volta, e poi entrare e uscire un certo numero di volte, e analogamente in quello di arrivo. Questi percorsi comprenderanno quindi due incroci dispari, ma tutti gli altri incroci saranno pari. Nell'itinerario rosso ci sono quattro incroci dispari, quindi non è possibile percorrerlo senza ripetere qualche tratto di strada, neanche finendo la passeggiata in un punto diverso da quello di partenza. In quello blu ci sono due incroci dispari: se è possibile percorrerlo senza ripetizioni, dovremo necessariamente partire da uno di essi e arrivare nell'altro; nell'itinerario verde, tutti gli incroci sono pari: possiamo quindi sperare di riuscire a percorrerlo partendo da un punto qualsiasi.

In effetti non si tratta solo di una speranza, ma si può dimostrare che per itinerari come quello blu o quello verde esiste sempre una passeggiata senza ripetizioni, ed esiste anche un semplice algoritmo per trovarne una.

Problemi di questo tipo vengono schematizzati con dei grafi, che sono formati da punti (i vertici del grafo) uniti da delle linee (gli spigoli del grafo): nei nostri esempi, i vertici corrispondono agli incroci e gli spigoli ai tratti di strada. In un grafo, ciò che conta è solo il tipo di connessione (cioè quali vertici sono collegati da quali spigoli), mentre non hanno alcuna importanza la posizione dei vertici e la lunghezza degli spigoli, o se questi sono diritti o curvi. I problemi proposti all'inizio, che equivalgono a stabilire se è possibile disegnare il grafo corrispondente senza mai sollevare la matita dal foglio e segnando ogni linea una sola volta, sono pertanto di carattere topologico; in effetti, spesso si fa risalire l'origine della topologia proprio a un celebre problema, quello dei ponti di Königsberg, di cui quelle presentate qui sono delle versioni “milanesi”.

Königsberg è l'antico nome di una città prussiana attraversata da un fiume nel quale ci sono due isole, collegate tra loro e alla terraferma da alcuni ponti. All'inizio del 1700 i suoi abitanti si chiesero se fosse possibile fare una passeggiata partendo da un punto qualsiasi della città e percorrendo tutti e sette i ponti allora esistenti una sola volta. Il matematico Eulero schematizzò il problema con un grafo, in cui i quattro vertici corrispondono alle zone della città (le due isole e le due rive del fiume) e i sette spigoli ai ponti che le congiungono. Fare un giro per la città attraversando una sola volta ciascuno dei sette ponti equivale al problema precedente: la passeggiata si può schematizzare con un grafo che ha quattro vertici dispari, dunque non è possibile percorrerlo come voluto. Lo stesso grafo si ritrova nel poster della mostra matemilano.

La teoria dei grafi, di cui Eulero pose le basi, si è sviluppata soprattutto dalla metà del secolo scorso ed ha numerose applicazioni in ricerca operativa, una branca della matematica che si occupa di problemi quali razionalizzare processi industriali, ottimizzare reti di distribuzione, gestire efficacemente un'impresa…
Spesso risolvere questi problemi è molto difficile; talvolta, poi, si conoscono solo degli algoritmi per trovare una soluzione, ma non si sa decidere se questa sia la migliore possibile: la loro complessità computazionale è così elevata che ci vorrebbe un numero enorme di anni affinché un calcolatore possa trovare una risposta.