There is a large variety of flowers whose petals are symmetrically arranged around the centre. 
Let us look, for example, at the periwinkle shown on the left, and fix our attention on one of its petals: we can pass from this one to any other by rotating the flower about its centre in such a way that each petal reaches one of the five possible positions.
The periwinkle has only these five rotations as symmetries.
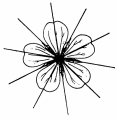
On the other hand, this other flower and also the one drawn here on the right has five reflections as well, reflections in each of the lines through the centre and the tip of a petal.
The pentagonal symmetry type is very common in the organic world: flowers apart, we can also find it in starfish and sea urchins. Apples and pears, too, have pentagonal symmetry: to see this, H.S.M. Coxeter suggests cutting an apple in the way you would cut an orange to squeeze out its juice, and look at its core.
Nature offers many examples of shapes that display a similar symmetry based on other numbers. For example, there are six rotations that transform a snow crystal into itself (and six reflections too), while there are three rotations (and three reflections) that transform a slice of banana or a courgette flower into itself.
In art there are extraordinary examples of buildings and patterns that are symmetrically arranged about a centre: the circular Pantheon in Rome, the octagonal Baptistry of the Cathedral in Florence, rose windows of Romanesque and Gothic churches, some mazes, Aztec calendars, and Indian mandalas.
A design is called a rosette if its symmetries are either only rotations or an equal number of rotations and reflections. In fact, it is not possible for a design to have different numbers of rotational and reflection symmetries. It appears that this conclusion was reached by Leonardo da Vinci when he was trying to determine all the possible symmetries of a building with a central plan.
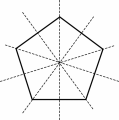
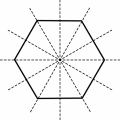From the mathematical point of view, the simplest rosettes are the regular polygons, that is those polygons with equal edges and equal angles. The snow crystals, for example, are nothing but magnificent elaborations of a single fundamental theme, the regular hexagon.
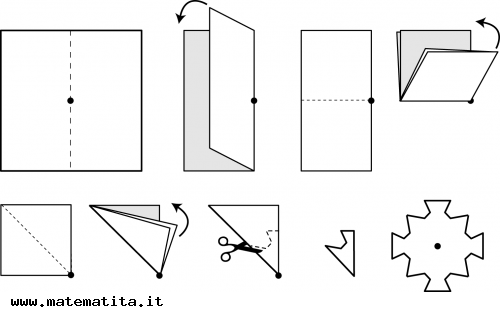
Would you like to make a paper model of a rosette?
Take a sheet of paper, fold it so that all the creases pass through the same point, and cut out a profile: by unfolding the paper you will have a rosette.
Note a rosette made in this way will always have both rotational and reflection symmetries.
Can you make one with only rotational symmetries?
by Paola Cereda
Transalated by Elisabetta Beltrami and Peter Cromwell