I poliedri regolari sono poliedri in cui sia i vertici, sia gli spigoli, sia le facce sono indistinguibili; e questa condizione è così forte che i poliedri regolari sono proprio pochi, soltanto cinque. Ma anche altri poliedri, pur non essendo regolari, ci possono colpire per la loro “simmetria”.

Qui a fianco in figura vediamo un pallone da calcio e, nella figura sotto, il poliedro che ha la stessa struttura; non è un poliedro regolare, perché le facce non sono tutte uguali fra loro - ci sono esagoni, ma anche pentagoni. Però esso ci appare con qualche forma di simmetria; le facce, pur non essendo tutte uguali fra loro, sono poligoni regolari e inoltre, se esaminiamo che cosa succede intorno a ogni vertice, ci accorgiamo che in tutti i vertici convergono un pentagono e due esagoni regolari. Potremmo immaginare di fare un calco in gesso intorno a un vertice e ottenere così una “formella”: la formella costruita per un qualsiasi vertice si adatterebbe poi perfettamente in corrispondenza di ogni altro vertice.

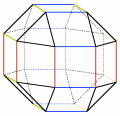
Il pallone da calcio è un esempio di poliedro uniforme, cioè di un poliedro in cui tutte le facce sono poligoni regolari e tutti i vertici sono “indistinguibili”; e proprio questa caratteristica dei vertici permette di identificare i poliedri uniformi con dei simboli numerici che indicano i poligoni che concorrono in ogni vertice: ad esempio (5,6,6) è il simbolo del pallone da calcio. 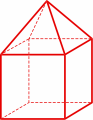Non potremmo usare un simbolo di questo genere, ad esempio, per identificare il poliedro qui a fianco, per il quale ci sono vertici in cui arrivano quattro triangoli, altri in cui arrivano due quadrati e due triangoli, e altri ancora in cui arrivano tre quadrati.

Ma cosa intendiamo dire esattamente con l’aggettivo “indistinguibile”? Dopo tutto i vertici sono dei punti, e
non c’è dubbio che tutti i punti siano uguali! Già l’esempio della formella però ci mostra che, quando parliamo di “cosa succede intorno a un vertice”, non stiamo prendendo in considerazione solo il punto, ma anche tutte le facce che arrivano in quel punto.

In realtà c’è un problema ancora più sottile e per dire che i vertici sono indistinguibili non è neppure sufficiente controllare con una formella che intorno a ogni vertice ci sia la stessa disposizione di facce.
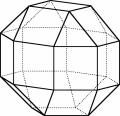
Il poliedro in figura qui a fianco (che prende il nome di poliedro di Miller) ha in ogni vertice tre quadrati e un triangolo equilatero e quindi una opportuna formella andrebbe bene per tutti i vertici. Eppure i vertici non sono indistinguibili! Possiamo accorgercene facendo riferimento all’anello di quadrati che corre lungo “l’equatore” del poliedro. C’è un solo anello di questo tipo (se partiamo da altre coppie di quadrati adiacenti non riusciamo a chiudere il giro) e due vertici possono non avere la stessa posizione rispetto a questo anello, come ad esempio i due vertici A e B in figura. 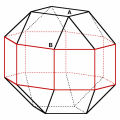Non si riuscirà mai a prendere in mano il poliedro di Miller e rigirarlo in modo che il vertice A si vada a trovare nella posizione occupata da B (e il poliedro appaia invece nella stessa posizione).

L’altro poliedro qui sotto “assomiglia molto” al poliedro di Miller, ma è “più simmetrico”: ci sono questa volta tre anelli di quadrati, e ciascun vertice appartiene a due di questi tre anelli. Con un po’ di pazienza si potrebbe verificare che (non solo la stessa formella si adatta a ogni vertice, ma, di più) comunque si scelgano due vertici è possibile trovare una simmetria del poliedro che manda il primo nella posizione occupata dal secondo. È questa la condizione che deve essere verificata per dire che si tratta di un poliedro uniforme (e per indicarlo con il simbolo (3,4,4,4)).