The photograph above shows the blue kaleidoscope, in which a
virtual cube can be produced, with a single ball placed in it.
The arrangement of the reflected images of the ball helps us to discover
the angles between pairs of mirrors of the kaleidoscope: there are some rings of four balls, and each of these corresponds to a pair of mirrors that meet at a right angle; there are some rings of six balls, corresponding to mirrors meeting at 60 degrees; finally, there are some rings of eight balls, which correspond to mirrors that meet at 45 degrees.
 We can recover these angles if we consider the sphere corresponding to the kaleidoscope.The surface of the sphere is divided into 48 "triangles", all equal to each other, whose angles are 90, 60 and 45 degrees - in fact there are vertices surrounded by four triangles (hence each of the four angles meeting there is 90=360/4 degrees), vertices surrounded by six triangles, and vertices surrounded by eight triangles.
We can recover these angles if we consider the sphere corresponding to the kaleidoscope.The surface of the sphere is divided into 48 "triangles", all equal to each other, whose angles are 90, 60 and 45 degrees - in fact there are vertices surrounded by four triangles (hence each of the four angles meeting there is 90=360/4 degrees), vertices surrounded by six triangles, and vertices surrounded by eight triangles.
 But 90+60+45 is 195, and not 180, so we have a triangle whose angles do not add up to 180 degrees! We should not be too surprised at this fact, because we are not really dealing with a proper triangle: it is a "fat" triangle, drawn on a sphere, whose edges are not straight lines, but the nearest thing that can be drawn on a sphere, that is arcs of great circles.
But 90+60+45 is 195, and not 180, so we have a triangle whose angles do not add up to 180 degrees! We should not be too surprised at this fact, because we are not really dealing with a proper triangle: it is a "fat" triangle, drawn on a sphere, whose edges are not straight lines, but the nearest thing that can be drawn on a sphere, that is arcs of great circles.
What kind of geometry applies to triangles on a sphere? What does it have in common with, and how does it differ from, the usual plane geometry that we are familiar with? We have just seen one difference: the sum of the angles of a triangle is no longer 180 degrees.
 Moreover, the angle sum is not even the same for all triangles: by examining the spheres corresponding to the other two kaleidoscopes, we can see that one sphere is divided into 24 triangles, all equal, each of which has one angle of 90 degrees and two of 60, while the other sphere is divided into 120 equal triangles, each of which has an angle of 90 degrees, one of 60, and one of 36. The sum of the angles in the first case is 210 degrees, in the second case it is 186 degrees.
Moreover, the angle sum is not even the same for all triangles: by examining the spheres corresponding to the other two kaleidoscopes, we can see that one sphere is divided into 24 triangles, all equal, each of which has one angle of 90 degrees and two of 60, while the other sphere is divided into 120 equal triangles, each of which has an angle of 90 degrees, one of 60, and one of 36. The sum of the angles in the first case is 210 degrees, in the second case it is 186 degrees.
| 186 | 6 | 1/120 |
| 195 | 15 | 1/48 |
| 210 | 30 | 1/24 |
The situation is summarised in the table above: the first column contains the sum of the angles of the triangle; the second column, the angular excess (that is by how much this sum exceeds 180 degrees); the third column, the area of the triangle as a fraction of the area of the sphere.
We can see that the larger the triangle, the larger is the sum of its angles.
For the triangles of the sphere corresponding to the red kaleidoscope, which are the smallest ones (their area is 1/120 of the area of the sphere), the angular excess is only 6 degrees.
For the triangles of the sphere corresponding to the blu kaleidoscope, which are larger (their area is 1/48 of the area of the sphere), the angular excess is 15 degrees.
Lastly, we have the triangles on the sphere corresponding to the yellow kaleidoscope: notice that each triangle is formed by two of the triangles on the "blue" sphere so the area is doubled; this time the angular excess is 30 degrees. So we see that doubling the area of a triangle also doubles its angular excess.
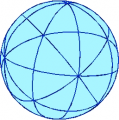
This is not a special case. One of the characteristics of the geometry on the sphere which distinguishes it from the usual geometry on the plane is the fact that similitude does not exist: that is we cannot - as on the plane - draw two figures with the same shape but of different sizes.
The size affects the shape, and vice versa: we cannot find a spherical triangle larger than the one shown here in the figure which also has the same angles.
Of course, we could start from a larger sphere, but if the angles are of 90, 60 and 45 degrees, the area of the triangle will still be 1/48 of the area of the sphere. In fact, the area of a spherical triangle is proportional to its angular excess.
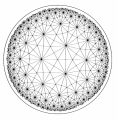
Are there also "thin" triangles besides "fat" ones? That is, are there triangles for which the sum of their angles is less than 180 degrees? The answer is yes, and the corresponding geometry is called hyperbolic geometry. The figure to the right (which recalls the structure of some drawings by Escher) is a companion of the spheres corresponding to the kaleidoscopes (and of the grids corresponding to the planar triangles): here too there are some "triangles" (thin ones), all equal to each other, and this time the angles are of 90, 60 and 360/14 degrees.
The interesting thing is that this situation is totally "symmetric" with respect to what we have seen before for the geometry on the sphere: again, in hyperbolic geometry, there is no similitude; the sum of the angles of a triangle is alway less than 180 degrees; the shape of a triangle determines its size; the area of a triangle is proportional to its angular defect, that is to how much the sum of its angles is less than 180 degrees. But this is just the beginning of a long story ...
