How many uniform polyhedra are there, and what is their structure?

To begin with, there are five regular polyhedra.

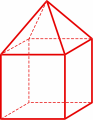
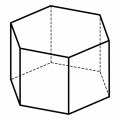Another standard example (more precisely a family of infinitely many examples) is given by prisms. A right prism with basis a regular polygon is a (4,4,...) uniform polyhedron as long as the height of the prism makes all the lateral faces squares.

There are infinitely many uniform polyhedra among prisms, one for every regular polygon which is fixed like its basis - in particular, if the basis is a square you get a cube). Here on the left you may see a (4,4,6).

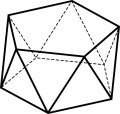
There is another family of polyhedra (maybe less known), which contains infinitely many uniform polyhedra: it is the family of antiprisms. Here on the right you may see a uniform antiprism of type (3,3,3,5): each vertex is adjacent to three equilateral triangles and a pentagon.
It is easy to imagine how you can get a uniform polyhedron if you start from any regular polygon and not just from a pentagon. In particular, if the basis is an equilateral triangle, you get the octahedron).

Are there other uniform polyhedra in addition to prisms, antiprisms and regular polyhedra? How many and which ones? In fact there are some of them, but not too many: thirteen all together, which are sometimes called archimedean polyhedra. If we want to list them, as we did for the others, with a numerical symbol, the full list can be given in the following table:

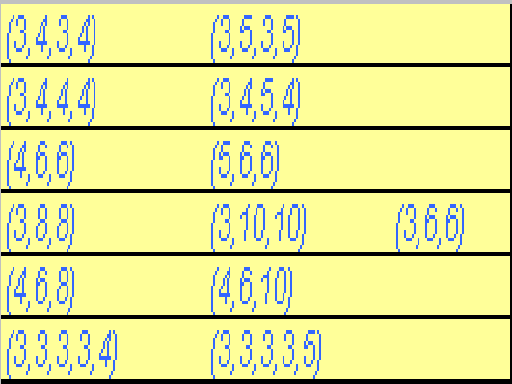
The table has been made following a pattern which can be useful to describe the corresponding polyhedra. The polyhedra in the first column are related to the cube, those in the second are related with the dodecahedron and those in the third column with the tetrahedron.

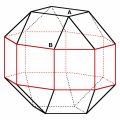
Almost all the polyhedra in the first column have the same symmetry of the cube. They can be seen in a kaleidoscope, in particular that associated with the cube. Only the polyhedron on the last row has a symmetry which is similar to that of a cube, but differs from it because it contains only rotations - thus it can not be seen in a kaleidoscope.

Analogously, all the polyhedra in the second column - except the last one -, scan be seen in the kaleidoscope of the dodecahedron; those in the last column can be seen in the kaleidoscope of the tetrahedron.

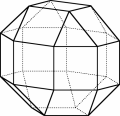
The row layout is not random. For instance, the (3,8,8) polyhedron represented below can be obtained from a cube by "smoothing" the vertices so that one gets equilateral triangles and regular octagons.
The other two polyhedra in the same row of the (3,8,8) are obtained in the same way, but starting from a different polyhedron. To obtain a (3,10,10) one starts from a dodecahedron and to obtain a (3,6,6) one starts from a tetrahedron.
Something similar occurs for the other rows of the table.

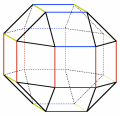
People who like numerical patterns may have noticed that the symbols of the second column can be obtained from the corresponding ones of the first column by substituting some "4" in "5" and some "8" in "10". How can we explain this phenomenon? And why is only the central "4" in (3,4,4,4) exchanged with a "5" and not the other two "4"? If you observe the polyhedra that you find below, you may find an answer...

Regular polyhedra are polyhedra where vertices, edges and faces can not be distinguished. This requirement is so strong that there are only five regular polyhedra. At any rate, other polyhedra - although not regular - can strike us for their symmetry.

Here on the left you may see football and, below, a polyhedron with the same structure. It is not a regular polyhedron because the faces are not all equal - there are hexagons and pentagons. Yet, it does have a symmetry. The faces - although not all alike - are regular polygons. Moreover, if we look at a vertex, we realize that at each vertex there are a pentagon and two hexagons. We can imagine to make a plaster cast around a vertex and obtain a sort of three-dimensional "stamp", which can be adapted to any other vertex.

The football is an example of a uniform polyhedron, i.e., a polyhedron which has faces that are regular polygons and all vertices can not be "distinguished". This latter property allows one to identify the uniform polyhedra with numerical symbols, which represent the polygons adjacent to every vertex. For instance, (5,6,6) is the symbol of the football.
We could not use a symbol of this type for the polyhedron here on the right. Indeed, it has vertices with four triangles, others with two squares and two triangles, and others with three squares.

What do we mean by saying that the vertices can’t be distinguished? After all, vertices are points and,
undoubtedly, all points are equal! Already the example of the "three-dimensional stamp" tells us something about all the faces adjacent to a vertex and not only the vertex!

Actually, the problem is even subtler, and to say that the vertices can’t be distinguished, it is not even enough that a three-dimensional "stamp" adapts to any vertex with the same arrangement of faces.

The polyhedron on the right (the Miller polyhedron) has three squares and an equilateral triangle at every vertex; so a convenient three-dimensional "stamp" would adapt to any vertex. Yet, the vertices can be distinguished!
It is possible to see it by looking at the chain of squares that rounds the "equator" of the polyhedron. There is just one chain of this type because, if we start from other pairs of adjacent squares , we can’t make a full round. So, two vertices may be distinguished because they do not have the same position with respect to this chain like, for instance, the two vertices A and B.
It is impossible to move the polyhedron so that the vertex A maps to the vertex B and the polyhedron stays in the same position.

The other polyhedron you may see below "looks like" the Miller polyhedron quite a lot, but it is "more symmetric". There are three chains of squares and each vertex belongs to two of these three chains. With a little bit of patience, you may verify that the same three-dimensional "stamp" adapts to any vertex. Furthermore, for any two vertices there exists a symmetry of the polyhedron which maps the two vertices one onto the other. This is the requirement which must be fulfilled to talk about a uniform polyhedron (and to denote it by the symbol (3,4,4,4)).