La classificazione delle superfici è un bel capitolo di matematica. Ci si pone un problema e si arriva a una risposta, completa e insieme relativamente semplice: e questa non è una cosa che accada frequentemente!
Qual è il problema?

Se vogliamo mettere in ordine degli oggetti (e sappiamo che questo è un problema che in matematica ci si pone spesso: non a caso un'intera sezione di questi "Per saperne di più" è dedicato al tema della classificazione), occorre fare due operazioni preliminari: specificare quali oggetti si vogliono mettere in ordine e dichiarare quali criteri si vogliono usare. Ad esempio, se si vuole ordinare i libri di casa propria, occorre decidere quali (Tutti? Solo quelli di chi li mette in ordine o anche quelli dei coabitanti? Solo quelli di lavoro o anche i romanzi? …) e come (per argomento? per data di pubblicazione? per casa editrice? per dimensione?…).
Partiamo allora col dire che cos'è una superficie. L'idea intuitiva che possiamo dare di superficie è quella di un qualcosa che, quando lo si vada a guardare da vicino, assomiglia a un piano. Pensiamo per esempio a una sfera; e, dicendo "sfera", ci riferiamo alla buccia di una palla, senza il suo interno; per chi si sente rassicurato da una scrittura analitica, stiamo pensando ai punti dello spazio le cui coordinate (x,y,z) verificano la condizione x²+y²+z²=1, mentre per l'intera palla, comprendente l'interno, dovremmo considerare i punti le cui coordinate verificano la condizione x²+y²+z² ≤ 1. Una sfera certamente non è un piano, e di questo non occorre convincere nessuno, ma se immaginiamo di fissare un punto della sfera e di fare uno zoom vicino a quel punto, beh, non è poi tanto diverso dallo zoom che potremmo fare vicino a un punto del piano (i matematici dicono "in un intorno" del punto). E, più andiamo avanti a zoomare, più i due intorni si assomigliano.
Se qualcuno ancora non è convinto, basta che pensi alla nostra comune abitazione, il pianeta Terra: sappiamo che si tratta di una sfera (approssimativamente), ma ce ne accorgiamo nella vita di tutti i giorni? In realtà, dato che in genere consideriamo solo un "piccolo intorno" della nostra posizione, ci sembra proprio di stare su un piano!
Naturalmente, per dare un senso preciso a questo discorso, dovremmo dire che cosa intendiamo dicendo che i due piccoli intorni "si assomigliano" (in "matematichese" diremmo che sono omeomorfi, ovvero che hanno la stessa forma, dal punto di vista della topologia: e si tratta proprio del criterio che useremo poi per la classificazione delle superfici). Cominciamo a farcene un'idea mostrando qualcosa che NON è una superficie, e quindi in cui gli intorni dei punti non assomigliano a un dischetto nel piano.

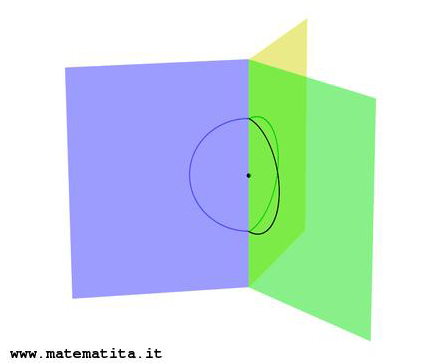
Pensiamo a una specie di libro con tre pagine, cioè tre semipiani che si attaccano lungo una retta, bordo comune di tutti e tre. Se si fa uno zoom vicino a un punto P di questa retta, si trovano sempre tre fogli che si attaccano lungo un lato, in figura tre semicerchi che si attaccano lungo un diametro. E, anche continuando a zoomare, non ne veniamo a capo: l'intorno di P resta sempre fatto in questo modo e quindi non "assomiglia" a un intorno di un punto del piano, cioè a un disco.
Quindi una sfera è una superficie, e cosí anche una ciambella o una doppia ciambella, mentre questa non lo è. E per il momento ci accontenteremo di questa distinzione.
Diciamo ora qualcosa di più circa i criteri rispetto ai quali vogliamo classificare le superfici: intanto chiariamo subito che i criteri che adottiamo non hanno nulla a che fare con i criteri rigidi a cui siamo abituati dalla geometria, con la misurazione di lunghezze o di aree: per esempio una sfera piccola o una sfera grossa sono per noi la stessa cosa; ma c'è di più: una sfera è la stessa cosa anche di un cubo, o di un icosaedro o (della buccia) di questa scultura bitorzoluta, o di quest'altra, o di quest'altra ancora. A patto sempre che si consideri solo la "buccia" degli oggetti in questione, come avevamo specificato per la sfera. Questo perché possiamo immaginare, per esempio, di passare dal cubo alla sfera con una trasformazione che non solo è un'applicazione biunivoca, ma che non introduce strappi, ovvero che è continua, sia all'andata che al ritorno (e proprio questo è quello che i matematici chiamano omeomorfismo: un'applicazione biunivoca, continua e tale che anche la sua inversa sia continua).
Spesso si sente dire che la topologia è la geometria della gomma: in effetti, se fissiamo le idee, per esempio, su un disco del piano, la topologia studia quelle proprietà del disco che restano invariate se si immagina di "stiracchiarlo" come si vuole, pensando naturalmente che sia fatto di materiale infinitamente elastico: con il divieto, però, di fare tagli o incollamenti. Ad esempio, consideriamo questa immagine di un disco, dove è in evidenza, in colore azzurro, la regione all'interno di una curva rossa, e sono segnati due punti, uno all'interno e uno all'esterno della stessa curva; confrontiamo ora questa immagine con un'altra dove lo stesso disco viene deformato con un omeomorfismo: ci si accorge allora che non ha nessun senso parlare di area, perché, ad esempio, l'area della regione in azzurro viene sicuramente modificata passando dal disco al suo deformato; ha senso invece, ad esempio, dire che il punto blu è all'interno e il punto giallo è all'esterno della curva rossa, perché questa caratteristica si mantiene anche quando il disco viene deformato.
Una cosa che è necessario specificare su queste deformazioni e stiracchiamenti è che siamo qui totalmente liberi: non solo siamo liberi di immaginare di essere dotati di un materiale talmente estensibile che un disco di raggio 1 cm si possa trasformare senza alcun problema in un disco di raggio alcune centinaia di anni-luce, ma anche (di più!) liberi rispetto a quei vincoli che ci sono imposti dall'abitare in un mondo tridimensionale. Per esempio, restando nel nostro mondo, non ci sarebbe alcuna maniera di trasformare questa superficie in una "normale" ciambella, come quest'altra.
Però questo è un problema che non dipende dalle due superfici "in sé", ma solo dall'ambiente in cui siamo: se fossimo in uno spazio a quattro dimensioni, saremmo in grado di manipolarle in modo da disporle in posizione identica.
Una maniera per tenere conto di questa maggiore libertà, (senza dover andare nello spazio a 4 dimensioni! e) senza rinunciare a immaginare le cose nel "nostro" mondo, è quella di pensare di avere a disposizione un'ulteriore possibilità: non solo deformare senza strappi, ma anche eventualmente tagliare, PURCHÉ, in un secondo momento, si vada a ricucire ESATTAMENTE gli stessi punti che si erano separati.
E, con queste "regole del gioco" è facile vedere che una ciambella annodata e una non annodata sono la stessa cosa: possiamo immaginare di tagliare la ciambella annodata lungo un meridiano, cominciare a staccare i due lembi della superficie che si uniscono lungo quella curva, allontanarli sempre più fino a sciogliere il nodo e ottenere un normale cilindro, da cui si può poi ricucire esattamente quello che prima avevamo tagliato: otteniamo la ciambella non annodata.
Fortunatamente esiste un oggetto, di uso comune, che ci rappresenta bene questa operazione di aprire e ricucire poi nella stessa posizione: si tratta della zip che viene usata per le chiusure di certi tessuti.
Un rettangolo con due zip nello stesso verso su due lati opposti si può richiudere a formare quello che tutti noi potremmo chiamare "cilindro", ma si può anche disporre diversamente per poi richiuderlo in modo da ottenere un oggetto a cui non sapremmo dare un nome e che certo non riusciamo a "manipolare" per far diventare un cilindro (nel nostro mondo a tre dimensioni; altrove ci riusciremmo!); però, aprendo la zip., possiamo facilmente manipolarlo e poi richiuderlo (cucendo insieme gli stessi punti che prima erano stati separati: e la zip ce ne è testimone!) in modo da ottenere un cilindro "normale". Quindi anche questo oggetto è omeomorfo a un cilindro, e la topologia (o, meglio, un omeomorfismo) non si accorge delle differenze fra i due.
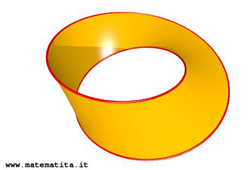
Un omeomorfismo vede invece la differenza fra il cilindro e un oggetto come questo, che in topologia si chiama nastro di Moebius e che si ottiene richiudendo un rettangolo con le zip sui due lati messe in versi opposti.
Un cilindro e un nastro di Moebius sono due cose diverse, anche rispetto a una relazione cosí lasca come l'omeomorfismo, e lo sono proprio "in sé", lo restano in qualsiasi ambiente li si vada a considerare, anche se fossimo in un mondo a 57 dimensioni!
Per accorgersene, si può per esempio seguire con un dito il bordo dell'oggetto e accorgersi cosí che, nel caso del nastro di Moebius il bordo è costituito da una sola curva, anche se abbiamo un nastro anomalo con tante, o tantissime torsioni (sempre un numero dispari!) mentre, nel caso del cilindro, il bordo è costituito da due curve, e questo continua a esser vero anche se si attorciglia il nastro, anche con tantissime torsioni (purché sempre un numero pari). Un altro modo per distinguere fra cilindri e nastri di Moebius è quello di tagliare l'oggetto lungo la curva centrale: nel caso di un cilindro, l'oggetto viene separato in due pezzi (eventualmente allacciati fra loro se il cilindro era un po' attorcigliato), mentre nel caso del nastro di Moebius si ottiene un pezzo solo (che può eventualmente risultare annodato).
Naturalmente, nel momento in cui volessimo rendere rigoroso questo discorso, dovremmo far vedere che questa proprietà di "essere di un pezzo solo" (in matematichese si dice essere connesso) è una proprietà topologica, ovvero si mantiene per omeomorfismo, cosí come ha un senso (topologico) il fatto di caratterizzare i punti del bordo. La sistemazione "rigorosa" di questi concetti non è poi cosí immediata, ma qui ci accontentiamo di un discorso informale.
Armati di zip, procediamo allora a dare un'idea del teorema di classificazione delle superfici: e le zip non sono poi cosí fuori luogo, dato che una recente dimostrazione di questo teorema, dovuta a Conway, in letteratura viene proprio chiamata zip proof.
Intanto, precisiamo cosa dice questo teorema: ogni superficie che gode di alcune caratteristiche – che discuteremo a momenti – deve essere necessariamente una superficie di questa lista di cosiddette superfici standard: la numero 0 (che è poi la sfera), la 1 (una ciambella, o toro) , la 2 (una doppia ciambella) , la 3, la 4, la 5, la 6, la 7, …; ed è anche chiaro come si possa continuare questa lista, individuando una superficie per ciascun numero naturale.
Le caratteristiche che deve verificare una superficie perché possiamo essere sicuri che sia (omeomorfa a) una della lista sono quattro: deve essere connessa, senza bordo, orientabile e compatta. Esaminiamole una ad una:

• "connessa" significa intuitivamente "fatta di un pezzo solo"; non ci interessa in questa lista una superficie fatta da una palla e una ciambella insieme: possiamo benissimo considerarla come una – sola! – superficie, perché verifica la condizione che abbiamo dato come distintiva di una superficie (lo zoom vicino a qualsiasi punto assomiglia a un disco); però non ci interessa perché, per l'appunto, se sappiamo come sono fatte tutte le superfici connesse, potremo poi dire che le non connesse sono fatte di diversi pezzi, ciascuno dei quali è una superficie della lista standard;
• "senza bordo" significa che escludiamo da questa lista le superfici come il cilindro, o il nastro di Moebius, o anche un disco (chiuso, cioè compresa la circonferenza di bordo); in tutti questi casi ci sono dei punti (i punti del bordo) in cui in qualche maniera la superficie "finisce" (in matematichese diremmo che sono punti che non hanno un intorno omeomorfo a un disco, ma piuttosto a un semidisco); anche in questo caso le escludiamo (in prima battuta) perché saremo poi capaci di descriverle a partire da quelle senza bordo: come si vede qui, un disco è la stessa cosa di una sfera a cui sia stato fatto un foro, mentre un cilindro è come una sfera con due fori;
• "orientabile" significa che NON contiene un nastro di Moebius; c'è in realtà un'analoga "lista" che comprende le superfici (compatte, connesse, senza bordo) non orientabili, ma qui non ce ne occupiamo; citiamo soltanto il fatto che tutte queste superfici non sono realizzabili nel mondo a tre dimensioni; riusciamo a realizzare quelle con bordo, come il nastro di Moebius, ma non quelle senza bordo;
• "compatta" ha un significato più tecnico che ci limitiamo a descrivere con qualche esempio, giusto per dare l'idea. L'intero piano, illimitato, non è compatto; non è compatto neanche un disco aperto, privo della circonferenza di bordo (l'insieme dei punti del piano per cui la distanza da un punto P fissato è strettamente minore di 1); invece una sfera è compatta; e anche un disco chiuso, comprendente la circonferenza di bordo (cioè l'insieme dei punti per cui la distanza da P è minore oppure uguale a 1) è una superficie compatta con bordo, e il bordo è proprio la circonferenza (cioè l'insieme dei punti per cui la distanza dal centro è uguale a 1).

Naturalmente tutte queste condizioni potrebbero essere descritte in maniera rigorosa (cosa che qui non faremo).
A questo punto possiamo enunciare il teorema di classificazione delle superfici: ogni superficie (compatta, connessa, orientabile, senza bordo) è omeomorfa a una superficie della lista di superfici standard.
Si sarebbe tentati di dire che ogni superficie è la stessa cosa di una ciambella con un po' di buchi, ma questa dicitura è pericolosa, e lo capiamo subito guardando un'immagine come questa, o quest'altra, o quest'altra ancora.
Ciascuna di queste superfici è omeomorfa a una di quelle della lista di superfici standard; ma a quale? Come facciamo a dire "quanti buchi hanno"? O, peggio ancora, domanda apparentemente innocua, ma in realtà molto intrigante: "che cos'è un buco?" Non avremmo avuto problemi a identificare che cos'è un buco e a contare i buchi nell'immagine di una superficie standard come questa, ma con queste altre superfici non solo non sappiamo contarli, ma addirittura ci viene il dubbio di non capire di cosa stiamo parlando. E ci fa apparire anche più strano il fatto che ogni superficie (con le caratteristiche che abbiamo detto) possa essere deformata in una della lista: sembrava cosí ovvio, ma ora non lo è più!
Il punto è abbastanza delicato e lo abbiamo già incontrato: quello che ognuno di noi chiamerebbe "buco" in una superficie come questa, in realtà, non è qualcosa di intrinseco alla superficie stessa (e che quindi ritroviamo in ogni altra superficie ad essa omeomorfa), ma dipende piuttosto dall'ambiente, da come la superficie è disposta nello spazio tridimensionale.
è meglio quindi non chiamarle ciambelle a 2 buchi, a 3 buchi, …, a n buchi, ma piuttosto superfici di genere 2, 3, … n. E che cos'è questo genere che, quando le superfici sono ben sistemate nella loro forma di ciambella, coincide con quello che ci appare come il "numero di buchi"?
Possiamo anche organizzare la stessa lista di superfici in un altro modo (apparentemente: in realtà, con gli occhiali della topologia, si tratta proprio degli stessi oggetti!): partendo sempre dalla sfera, cominciamo a attaccare alla sfera un manico, e poi 2 manici, 3, 4, 5, 6, 7, 8; e quindi lo stesso numero che abbiamo chiamato genere appare in questa descrizione come il numero dei manici.
Siamo quindi alla ricerca di una definizione di genere che possiamo riconoscere come avente a che fare con il numero dei "buchi" quando la superficie è "sistemata" nella forma di ciambella, e con il numero dei manici quando la stessa è "sistemata" nella forma di sfera con manici; e magari questa stessa definizione potrebbe darci un'idea di perché queste superfici siano la stessa cosa, e anche di come facciamo a riconoscere quelle più strambe come questa.
Una possibile definizione è la seguente: il genere di una superficie è il massimo numero di curve disgiunte semplici e chiuse che possiamo disegnare su questa superficie, immaginando di effettuare un taglio lungo queste curve, e senza tagliare la superficie in due pezzi.
Dire ad esempio che questa superficie ha genere 2 significa che è possibile trovare due curve messe in modo tale che, tagliando la superficie lungo queste due curve, questa non si separa in due pezzi; mentre qualunque taglio successivo (lungo una curva semplice e chiusa che non intersechi le precedenti) taglia invece la superficie in due.
Non dovrebbe essere difficile convincersi che, nel caso delle ciambelle a n buchi, il genere è proprio il numero n dei "buchi", e, nel caso delle sfere a n manici, il genere è proprio il numero dei manici.
Ma c'è di più: il genere ci può aiutare a capire perché, per esempio, una sfera a 3 manici e una ciambella a 3 buchi sono la stessa cosa (dal punto di vista della topologia). Immaginiamo di tagliare la sfera a 3 manici lungo 3 curve, ciascuna delle quali tagli uno dei manici a metà strada: possiamo poi far "rientrare" i manici e quello che otteniamo è una sfera con sei fori (nel senso che dalla sfera sono stati rimossi sei piccoli dischetti). Immaginiamo ora di tagliare una ciambella a 3 buchi lungo 3 curve; con un po' più di fatica ci rendiamo conto che quello che otteniamo è ancora una sfera con sei fori: la sfera sarà un po' bitorzoluta, ma di questo la topologia non si preoccupa!
Merita un'osservazione a parte la sfera, che ha genere 0; dire che la sfera ha genere 0 equivale a dire una cosa che sembra ovvia, ma che non lo è affatto, e cioè che qualunque curva semplice e chiusa sulla sfera la separa in due pezzi. Traslando questa affermazione sul piano (dopotutto, dal punto di vista della topologia, sfera e piano sono certo diversi, ma basta togliere un punto alla sfera per ottenere qualcosa che è omeomorfo a un piano), si ottiene il famoso teorema di Jordan: ogni curva semplice e chiusa nel piano lo divide in due pezzi, un interno, limitato, e un esterno, illimitato. Si tratta di un'affermazione che sembra "ovvia" e intuitiva; in realtà si fa addirittura fatica a capire che ci sia l'esigenza di dimostrare qualcosa. 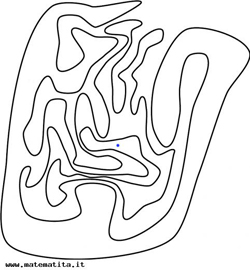Anche quando la curva è cosí arzigogolata che non è semplice per esempio individuare a occhio se il punto segnato in blu sta all'interno o all'esterno della curva stessa, non mettiamo tuttavia in dubbio il fatto che ci siano solo queste due possibilità: e ci basta colorare la regione dove sta il punto per accorgersi se è l'interno o l'esterno! Eppure, giustificare in maniera rigorosa il teorema di Jordan non è cosa da poco: come spesso accade, o si usano strumenti assai sofisticati e si riesce cosí ad avere una dimostrazione semplice, oppure, con strumenti elementari, la dimostrazione risulta macchinosa, molto più macchinosa di quel che l'enunciato cosí semplice farebbe sospettare.
Abbiamo a questo punto una strategia per riconoscere una superficie "strana": proviamo a tagliarla, lungo curve semplici e chiuse, finché non arriviamo a una sfera con un certo numero di fori (un numero che sarà un numero pari, perché ogni taglio produce due fori): ricucendo – per esempio immaginando di lasciare delle zip dove avevamo tagliato e chiudendo poi le zip – si trova che la superficie è omeomorfa a una della lista.
Tutto bene, ma? Come facciamo a essere sicuri che a furia di tagliare si arriva sempre e comunque alla situazione di una sfera con un po' di fori? Succederà anche con superfici veramente strane come alcune di quelle che abbiamo mostrato? In effetti la risposta è sí, e a questo punto possiamo immaginarcelo, ma… una giustificazione rigorosa è un'altra storia!