Reflections
Many everyday objects have bilateral symmetry: furnishings, lamps, road signs, flags, musical instruments and some of our clothes (but not individual gloves, or shoes). So do many animals and leaves; even the human body in its external form has approximate bilateral symmetry (though it would be different if we considered the internal organs too).
What does the phrase "this butterfly has bilateral symmetry" or "this butterfly has a plane of symmetry" mean?
Imagine cutting something in half along a plane and putting a mirror in place of this plane. If the reflected image together with the original half reconstructs the whole object then the plane is a mirror plane or plane of reflection symmetry.
In practice, it can be rather hard to cut a fork in half, not to mention a butterfly or a human being (even if the imagination of Italo Calvino tried it in the novel "The Cloven Viscount"). It is easier to do analogous experiments with planar figures, in which case mirror symmetry is no longer defined by a plane, but by a straight line.
To check whether a particular straight line is a line of reflection symmetry (mirror line) of a figure, we can place a mirror along the line and hold it perpendicular to the plane of the figure. For the line to be a mirror line, the reflected image together with half the original must reconstruct the whole object. As you can see from the two figures below, this need not happen, even if the straight line divides the figure into equal parts.
What happens when we use two mirrors?
Suppose, for example that we place a "p" between two parallel mirrors: then you can see a series of images which repeat along a strip, alternating images of "p" with images of "q".
If we make first a reflection with respect to a straight line, and then another reflection with respect to another line parallel to the first one, the combined effect is equivalent to that of a traslation, in the direction perpendicular to the two mirror lines, and of a distance twice the distance between the two mirrors.
A reflection exchanges the right with the left: in fact the mirror image of a "p", which has a tail on the left-hand side, is a "q", with a tail on the right. A translation, instead, corrisponds to two reflections and so ... the tail of the "p" comes back to its place!
What happens if the mirror lines are not parallel but meet?
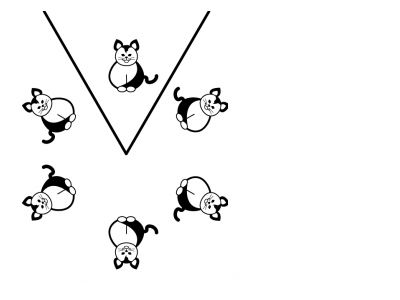
Placing an object between two connected mirrors (as shown in the figure, a cat with its tail on the right), you can see some images of the object, and, among these, those with the tail on the left alternate with those with the tail on the right. The images are no longer positioned along a strip, but around a centre, instead. In effect, if we make first a reflection with respect to a straight line, and then another reflection with respect to another line which has a point in common with the first one, the effect obtained is equivalent to a rotation about this point, by an angle twice the angle between the mirror lines.
How many images are seen?
If the angle between the mirrors is a submultiple of 180 degrees, as in the figure here (where the angle is 60 degrees) then the 360 degree angle is divided by the mirrors - both real and virtual ones - into an even number of angles (six in the figure) each of which contains an image: half of them (three in the figure) contain an image obtained from the original object by rotation (and so the cat has its tail on the right), while the others are obtained from the original object by reflection (and so the cat has its tail on the left).
