In questa scheda sono presentati gli oggetti della mostra Simmetria, giochi di specchi e le schede che li accompagnano.

L'idea-chiave della mostra è visivamente "riassunta" nei cinque cartelloni intitolati "Simmetria". Le immagini dei primi tre, pur molto diverse fra loro, richiamano tutte, per qualche verso, la simmetria: dai mosaici arabi dell'Alhambra, ai paesaggi delle Montagne Rocciose riflessi nelle acque di un lago, ai merletti, ai fiori. Negli altri due cartelloni sono riportate solo alcune tra queste immagini: in particolare, quelle che possono essere "fabbricate" in una camera di specchi. E queste ultime sono "catalogate" a seconda della forma della camera in cui possono essere ricostruite.

Le tre camere di specchi triangolari che si trovano sui tavoli della mostra sono quindi in un certo senso il fulcro di tutto il percorso proposto. Ciascuna di esse è costituita da tre specchi perpendicolari al piano del tavolo su cui è appoggiata e stacca su questo piano un triangolo: un triangolo equilatero, un triangolo rettangolo isoscele e un triangolo rettangolo con angoli di 30 e 60 gradi.
L'obiettivo principale che la mostra si pone è quello di condurre il visitatore a intuire quale "parentela" ci sia fra i disegni ottenuti nella stessa camera di specchi e in che cosa consista invece la diversità di disegni ottenuti in camere di specchi di forma differente.

Per guidare il visitatore a trovare le risposte, sono suggeriti alcuni problemi: sulle pareti di ogni camera sono illustrate pavimentazioni che è possibile ricostruire nella camera stessa (pur di trovare le piastrelle giuste da inserire tra gli specchi) e su fogli a parte ne sono proposte altre per le quali non viene neanche specificata la camera in cui lavorare. Così, per gradi, si arriva ad intuire qual è il tipo di simmetria che "governa" un dato disegno.

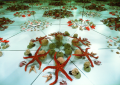
In realtà non soltanto questi problemi sulle pavimentazioni aiutano a cogliere il tipo di simmetria comune ai diversi disegni riprodotti in ciascuna delle camere di specchi: la "parentela che intercorre fra le maniere in cui si ripetono le immagini riflesse in una data camera sussiste qualunque sia l'oggetto posto fra le pareti, anche una sciarpa o un mazzo di fiori o qualche pallina...
Le griglie appese sopra le scatole triangolari chiariscono bene quello che succede: vi è messo in evidenza un triangolo (che rappresenta la camera di specchi) e la griglia stessa (illimitatamente prolungata) rappresenta ciò che si vede nella camera quando non vi si mette nulla.

Per capire la geometria sottostante ai disegni illimitati che si formano nelle camere degli specchi, è utile incominciare analizzando ciò che accade con un solo specchio oppure con due specchi: un tavolo della mostra propone l'uso di uno specchio per cercare gli assi di simmetria di un disegno; altri presentano due specchi paralleli o due specchi incidenti per guidare all'osservazione della composizione di due riflessioni. A tali argomenti sono dedicate anche le schede 1, 2 e 3.

Ci sono anche due camere di specchi più piccole, con una base quadrata: il visitatore può disegnare quello che vuole e osservare direttamente "l'effetto che fa" inserendo il suo disegno nella camera di specchi.

I tre cartelloni sui mosaici completano il discorso per chi vuole saperne di più: essi mostrano 17 tipi diversi di simmetria per un mosaico, ovvero per un disegno che si ripeta periodicamente nel piano in più di una direzione (esempi di alcuni di questi 17 tipi sono dati dalle pavimentazioni che si vedono nelle camere di specchi).
Il fatto che questi 17 siano i soli possibili è un risultato matematico profondo, e non banale; ed è, per certi versi, sorprendente che artisti di ogni parte del mondo siano arrivati a dare esempi di ciascuno di questi casi anche molto prima che i matematici affrontassero questo problema.
Le schede 4 e 5 approfondiscono il discorso sulle pavimentazioni piane, mentre la scheda 6 si occupa dei 17 tipi di simmetria dei mosaici.

Una situazione analoga a quella descitta per i mosaici si ha per i disegni che si ripetono periodicamente in una sola direzione, i cosidetti fregi: qui ci sono solo sette possibilità illustrate anch'esse in un cartellone. In una bacheca si può vedere come tutte queste possibilità si possano riottenere tagliando una striscia di carta opportunatamente piegata o arrotolata. Le schede 7 e 9 riprendono questi argomenti, metre la scheda 8 illustra alcune realizzazioni dei sette fregi nell'artigianato africano.

E' naturale domandarsi se si possono usare gli specchi anche per classificare il tipo di simmetria di oggetti solidi. La risposta è suggerita dai tre caleidoscopi tridimensionali che costituiscono un altro punto focale della mostra.

Essi "funzionano" in un modo del tutto analogo alle tre scatole di specchi triangolari: se un oggetto (ad esempio una pallina) viene inserito nel caleidoscopio, le sue immagini riflesse si dispongono intorno a un centro e formano "qualcosa" di tridimensionale.
Sopra ciascuno dei caleidoscopi è appesa una palla suddivisa in triangoli (sferici) tutti uguali fra loro. Essa rappresenta per il caleidoscopio l'analogo di quello che è la griglia per una camera di specchi piana: se immaginiamo uno di questi triangoli "foderato" di specchi (ogni specchio rappresenta un piano che passa per il centro della palla e per uno dei lati del triangolo) otteniamo il caleidoscopio corrispondente.
La scheda 10 propone un approfondimento del legame tra la situazione bidimensionale e quella tridimensionale.

Disponendo oggetti diversi nello stesso caleidoscopio si ottengono immagini differenti, ma con lo stesso tipo di simmetria (mentre in caleidoscopi diversi si vedono immagini con simmetria diversa). Questa osservazione può essere fatta a partire da oggetti qualsiasi (e una pallina è particolarmente istruttiva per vedere quante immagini si formano e come esse sono disposte): in particolare, di fianco ad ogni caleidoscopio si trovano dei "mattoncini" che portano a vedere nel caleidoscopio alcuni poliedri, fra cui quelli regolari, che peraltro sono illustrati anche nei tre cartelloni corrispondenti ai caleidoscopi.

Ma come si fa, per esempio nel caso di un cubo, a individuare sia la forma del caleidoscopio che la forma del pezzo che va inserito in esso in modo da ricostruire un cubo intero? Su un altro tavolo della mostra si cerca di far intuire la genesi di questo "mattoncino" presentando tre coppie di specchi incidenti, ad angoli diversi, e vari poliedri che rappresentano delle frazioni di cubo. Appoggiando (nel modo giusto...!) uno di questi poliedri a uno specchio (se è la metà di un cubo) o a due specchi (negli altri casi), si vede il cubo intero: indicazioni più precise si trovano nelle schede 11 e 12.

Ci sono nella mostra anche caleidoscopi tridimensionali piccoli, ma in essi non va inserito alcun oggetto, perchè sono già stati tagliati sul fondo in modo che sia possibile vedere un certo poliedro. Se si osserva bene, si nota che quelli dello stesso colore sono "parenti", nel senso che gli angoli fra i vari specchi sono gli stessi, e varia solo il modo con cui essi sono tagliati sul fondo: i poliedri che si vedono possono essere tutti ricostruiti nel caleidoscopio grande del colore corrispondente (a patto di trovare il pezzo giusto da inserire...).
Chi voglia approfondire il discorso sui poliedri può trovare del materiale nelle schede 13, 14, 15, 16, 17, 18 e 19.
La scheda 20 tratta invece il tema della simmetria in natura.