The family of symmetries of the cube

The 48 symmetries of the cube form a family with interesting properties. It is a very closed family: the result of the composition of two or more elements of the family is still a member of the family.

The identity transformation has an exceptional role in it. It is the neutral element of the family, in the sense that any symmetry of the cube composed with the identity remains itself.

In general the order in which you compose the transformations affects the final result.
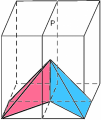
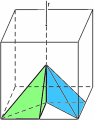
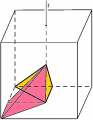
For example, in the two figures on the left we see where the reference pyramid moves if we first reflect the cube with respect to the plane p and then we rotate it of 1/4 of turn about the line r. In the other two figures on the rigth, we see where the pyramid moves if we reverse the order of composition.

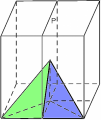Any symmetry of the cube has a mischievous twin with which it has a privileged relationship. The mischievous twin undoes the symmetry by moving the reference pyramid back to the start. It is called the inverse of the symmetry. When a symmetry is combined with its inverse, independent of the order, the result is the identity. For example, the rotation of 1/4 of turn about the line r has as its inverse the rotation of 3/4 of turn about r; any reflection is its own inverse; the composition represented in the figures above, reflection in the plane p followed by a rotation of 1/4 of turn about r, has as its inverse the composition of a rotation of 3/4 of turn about r followed by reflection in the plane p -- in this order! This is the same as when you reverse the operation "put on socks then put on shoes", first you take off shoes then you take off socks, not vice versa!

Any symmetry of the cube composed with itself a certain number of times gives the identity. For example, the reference pyramid goes back to its initial position if we perform four times a rotation of 3/4 turn about a line joining the centres of two opposite faces, or if we repeat twice a reflection in a mirror plane.

In describing the characteristics of the family of symmetries of the cube we have given an example of one of the most important concepts in mathematics: the structure known as a group.
The symmetries of the cube, with the operation given by performing first one and then the second (composition), constitute a group. Another example of group is given by the set of (positive and negative) integers, with the operation of sum.
This family too is closed (the sum of two integers is still an integer); the number 0 has the same role as the identity transformation has for the family of symmetries of a cube (the sum of any number and zero is equal to the starting number); and for any number, its relative with which it has a privileged relationship is the number of opposite sign (any number summed with its opposite is zero).

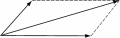The group structure is found in many other contexts: for example, the set of vectors in the plane with the combination rule given by the parallelogram rule for the sum of two vectors is a group.

Not only the symmetries of a cube, but also the symmetries of any plane figure or of any solid object form a group with the operation of composition, just like in the case of the cube.
If the starting shape is completely asymmetric, the symmetry group is the group containing a single element: the identity.

The symmetry group of the plane figure on the left has 6 elements. (Which ones? What is the inverse of each element?)

Rosettes are plane figures whose symmetry group contains a finite number of elements. There are also some figures whose symmetry group contains infinitely many elements, for example a circle or a straight line.