triangoli sferici e triangoli piani
Triangoli sferici e triangoli piani

La fotografia qui sopra rappresenta tre (sole!) palline nel caleidoscopio in cui si riesce a vedere un cubo. La disposizione delle immagini riflesse delle palline ci aiuta a scoprire gli angoli fra due specchi del caleidoscopio: le palline gialle (virtuali) si dispongono in anelli di quattro, perché la pallina gialla (reale) è in corrispondenza di due specchi che si uniscono a 90 gradi; analogamente gli anelli di sei palline blu ci dicono che la pallina blu è in corrispondenza di due specchi che si uniscono a 60 gradi e gli anelli di otto palline rosse che quella rossa è in corrispondenza di due specchi che si uniscono a 45 gradi.
 Ritroviamo gli stessi angoli se consideriamo la sfera corrispondente al caleidoscopio; la superficie della sfera è divisa in 48 “triangoli”, tutti uguali fra loro, i cui angoli sono di 90, 60 e 45 gradi: infatti, ci sono vertici dove arrivano quattro triangoli (quindi ciascuno dei quattro angoli che si incontrano qui è di 90°=360°/4), vertici dove ne arrivano sei, vertici dove ne arrivano otto.
Ritroviamo gli stessi angoli se consideriamo la sfera corrispondente al caleidoscopio; la superficie della sfera è divisa in 48 “triangoli”, tutti uguali fra loro, i cui angoli sono di 90, 60 e 45 gradi: infatti, ci sono vertici dove arrivano quattro triangoli (quindi ciascuno dei quattro angoli che si incontrano qui è di 90°=360°/4), vertici dove ne arrivano sei, vertici dove ne arrivano otto.
 Ma: 90+60+45 fa 195, e non 180: abbiamo quindi un triangolo la cui somma degli angoli non è 180 gradi! Questo però non ci deve stupire troppo, perché non si tratta proprio di un triangolo: è un triangolo “grasso”, disegnato su una sfera, i cui lati non sono segmenti bensì la “cosa” più vicina ai segmenti che possa essere disegnata su una sfera, cioè archi di cerchio massimo.
Ma: 90+60+45 fa 195, e non 180: abbiamo quindi un triangolo la cui somma degli angoli non è 180 gradi! Questo però non ci deve stupire troppo, perché non si tratta proprio di un triangolo: è un triangolo “grasso”, disegnato su una sfera, i cui lati non sono segmenti bensì la “cosa” più vicina ai segmenti che possa essere disegnata su una sfera, cioè archi di cerchio massimo.
Come è fatta la geometria dei triangoli sulla sfera? Che cosa ha di uguale e che cosa di diverso rispetto alla normale geometria piana che conosciamo? Una differenza è questa che già abbiamo visto: la somma degli angoli di un triangolo non è più di 180 gradi.  E non è nemmeno sempre la stessa per ogni triangolo: esaminando le sfere corrispondenti agli altri due caleidoscopi, ci accorgiamo che una è divisa in 24 triangoli, tutti uguali fra loro, ciascuno dei quali ha un angolo di 90 gradi e due di 60, mentre l’altra è divisa in 120 triangoli, tutti uguali fra loro, ciascuno dei quali ha un angolo di 90 gradi, uno di 60 e uno di 36. La somma degli angoli nel primo caso è di 210 gradi, nel secondo caso di 186.
E non è nemmeno sempre la stessa per ogni triangolo: esaminando le sfere corrispondenti agli altri due caleidoscopi, ci accorgiamo che una è divisa in 24 triangoli, tutti uguali fra loro, ciascuno dei quali ha un angolo di 90 gradi e due di 60, mentre l’altra è divisa in 120 triangoli, tutti uguali fra loro, ciascuno dei quali ha un angolo di 90 gradi, uno di 60 e uno di 36. La somma degli angoli nel primo caso è di 210 gradi, nel secondo caso di 186.
| 186 | 6 | 1/120 |
| 195 | 15 | 1/48 |
| 210 | 30 | 1/24 |
La situazione è riassunta nella tabella qui a fianco, in cui la prima colonna rappresenta la somma degli angoli del triangolo, la seconda l’eccesso angolare (ossia di quanto questa somma è maggiore dell’angolo piatto) e la terza l’area del triangolo rispetto all’area della sfera.
Possiamo osservare che più il triangolo è grande, più è grande la somma degli angoli. Per i triangoli della sfera corrispondenti al caleidoscopio rosso, che sono i più piccoli (la loro area è 1/120 dell’area della sfera) l’eccesso angolare è di soli sei gradi. Per i triangoli della sfera corrispondenti al caleidoscopio blu, che sono più grandi (la loro area è 1/48 dell’area della sfera) l’eccesso angolare è di quindici gradi. Infine, per i triangoli della sfera corrispondenti al caleidoscopio giallo, che sono esattamente il doppio dei precedenti (se accostiamo lungo il cateto maggiore due dei triangoli della sfera corrispondente al caleidoscopio blu otteniamo uno dei triangoli della sfera corrispondente al caleidoscopio giallo) l’eccesso angolare è di trenta gradi. Troviamo quindi, per un triangolo di area doppia, un eccesso angolare doppio.
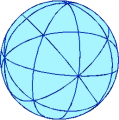 Questo non è un caso. Una delle caratteristiche della geometria sulla sfera più distante dalla geometria euclidea a cui siamo abituati è il fatto che non esiste la similitudine: non possiamo cioè - come sul piano - disegnare due figure che abbiano esattamente la stessa forma, ma siano una un po’ più grande e l’altra un po’ più piccola. La dimensione condiziona la forma, e viceversa: non possiamo trovare un triangolo sferico che sia più grande di quello qui in figura e che abbia gli stessi angoli. Possiamo naturalmente partire da una sfera più grande, ma se gli angoli sono di 90, 60, 45 gradi, l’area del triangolo sarà comunque 1/48 dell’area della sfera. L’area di un triangolo è in effetti proporzionale al suo eccesso angolare.
Questo non è un caso. Una delle caratteristiche della geometria sulla sfera più distante dalla geometria euclidea a cui siamo abituati è il fatto che non esiste la similitudine: non possiamo cioè - come sul piano - disegnare due figure che abbiano esattamente la stessa forma, ma siano una un po’ più grande e l’altra un po’ più piccola. La dimensione condiziona la forma, e viceversa: non possiamo trovare un triangolo sferico che sia più grande di quello qui in figura e che abbia gli stessi angoli. Possiamo naturalmente partire da una sfera più grande, ma se gli angoli sono di 90, 60, 45 gradi, l’area del triangolo sarà comunque 1/48 dell’area della sfera. L’area di un triangolo è in effetti proporzionale al suo eccesso angolare.
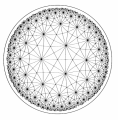 Esistono anche triangoli “magri”, oltre ai triangoli grassi? Ovvero triangoli in cui la somma degli angoli è minore di 180 gradi? La risposta è affermativa, e la geometria corrispondente è la geometria iperbolica. La figura più sotto (che ricorda la struttura di certi disegni di Escher) è una “sorella” delle sfere corrispondenti ai caleidoscopi (e delle griglie corrispondenti ai triangoli piani): anche qui ci sono dei “triangoli”(magri), tutti uguali fra loro, e questa volta gli angoli sono di 90°, 60° e (360/14)°
E “il bello è” che la situazione è totalmente “simmetrica” rispetto a quello che abbiamo visto prima per la geometria della sfera: anche in geometria iperbolica non c’è la similitudine, la somma degli angoli di un triangolo è sempre minore di un angolo piatto, la forma di un triangolo determina la sua grandezza, e l’area di un triangolo è proporzionale al suo difetto angolare, ossia a quanto la somma degli angoli è minore della misura di un angolo piatto.
Ma questo è solo l’avvio di una lunga storia …
Esistono anche triangoli “magri”, oltre ai triangoli grassi? Ovvero triangoli in cui la somma degli angoli è minore di 180 gradi? La risposta è affermativa, e la geometria corrispondente è la geometria iperbolica. La figura più sotto (che ricorda la struttura di certi disegni di Escher) è una “sorella” delle sfere corrispondenti ai caleidoscopi (e delle griglie corrispondenti ai triangoli piani): anche qui ci sono dei “triangoli”(magri), tutti uguali fra loro, e questa volta gli angoli sono di 90°, 60° e (360/14)°
E “il bello è” che la situazione è totalmente “simmetrica” rispetto a quello che abbiamo visto prima per la geometria della sfera: anche in geometria iperbolica non c’è la similitudine, la somma degli angoli di un triangolo è sempre minore di un angolo piatto, la forma di un triangolo determina la sua grandezza, e l’area di un triangolo è proporzionale al suo difetto angolare, ossia a quanto la somma degli angoli è minore della misura di un angolo piatto.
Ma questo è solo l’avvio di una lunga storia …