Per sapere cosa succede in uno spazio quadridimensionale è sufficiente affidarsi all'analogia con lo spazio tridimensionale?

L'analogia ci permette di accedere alla quarta dimensione anche se in realtà non possiamo “vederla”. Ci permette anche di scoprire fenomeni originali: ad esempio possiamo affermare che in uno spazio quadridimensionale non ci sarebbe più privacy, in quanto si potrebbe vedere all'interno di ogni edificio (se supponiamo ogni edificio ancora come tridimensionale). Tale asserzione, a prima vista bizzarra, diventa plausibile se ragioniamo con l'analogia. Se vivo in uno spazio bidimensionale posso toccare un cerchio, ma non posso guardare al suo interno; ho bisogno di una dimensione supplementare per potermi alzare “al disopra” del cerchio. Cosi' nello spazio non posso guardare all'interno di un cubo; ma se aggiungo una dimensione...il gioco è fatto!

Questo non significa però che l'analogia, da sola, sia sufficiente e adatta per affrontare in toto lo studio della quarta dimensione. Anzitutto l'analogia ci può magari aiutare a “predire” che cosa avviene in uno spazio quadridimensionale, ma in generale non ci fornisce anche una dimostrazione; in altre parole, ci permette di formulare delle congetture, ma in generale non permette di affermare con certezza se quello che abbiamo previsto sia vero o no. L'analogia può addirittura trarre in inganno. La circonferenza di un cerchio di raggio r è 2πr, la superficie di una sfera di raggio r è 4πr². Si potrebbe quindi pensare che la superficie esterna di un'ipersfera di raggio r (che si può definire come l'insieme dei punti dello spazio quadridimensionale a distanza r da un punto fissato) sia di 6πr³ o 8πr³; e invece vale 2πr³...

In altri casi l'analogia è quanto meno poco evidente; immaginate di deformare (ma senza tagliare) il nodo a sinistra; non potrete mai ottenere il nodo a destra, mentre si può dimostrare che nello spazio quadridimensionale ciò è possibile.

Ci sono poi fenomeni dove l'analogia proprio non può aiutarci nella speculazione sugli spazi di dimensione più grande di tre; un esempio è dato dai politopi regolari che, intuitivamente, rappresentano la generalizzazione n-dimensionale dei poligoni e poliedri regolari.
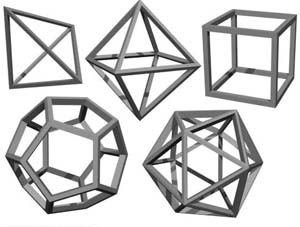
Esistono un infinità di poligoni regolari, mentre esistono solo cinque poliedri regolari, i solidi platonici.

In dimensione 4 ne esistono sei e per ogni dimensione più grande di 4 ne esistono sempre e soltanto tre... A partire dal caso dei poligoni e dei poliedri non avremmo certo potuto immaginarlo!

A cura di Paolo Bellingeri per la mostra Un tuffo nella quarta dimensione.