Dove si vede una certa regolarità, e insieme compare anche il numero 5 (e un icosaedro è allora proprio il posto giusto…!), si può immaginare che spunti in qualche modo il rapporto aureo… e non si immagina certo male!

L’icosaedro è davvero pieno di rapporti aurei! Innanzitutto i suoi spigoli, che sono trenta, si possono dividere in cinque gruppi, di sei spigoli l’uno (nella foto, i cinque gruppi sono messi in evidenza dal colore), in modo tale che un singolo gruppo di sei spigoli – ad esempio, quelli gialli nella foto – sia composto da tre coppie di spigoli paralleli fra loro (e opposti nell’icosaedro), che sono anche i lati opposti di un rettangolo aureo. E il fatto che i rettangoli siano proprio aurei si vede immediatamente quando si considerano i pentagoni regolari ottenuti tagliando l’icosaedro lungo un piano che contiene i cinque vertici adiacenti a un vertice fissato: i rettangoli di cui si diceva hanno due lati opposti che sono (spigoli dell’icosaedro e) lati di questo pentagono e gli altri due che ne sono diagonali (e sappiamo che il rapporto aureo è il rapporto fra diagonale e lato di un pentagono regolare).

Si possono quindi individuare tre rettangoli aurei nell’icosaedro, e questo si può fare in cinque modi diversi, ottenibili l’uno dall’altro per rotazione dell’icosaedro intorno a un asse che passa per due vertici opposti; facendo riferimento a questa foto, una tale rotazione potrebbe ad esempio mandare i sei spigoli rossi nei sei gialli, questi nei sei blu, ecc. Prendendo in considerazione una sola di queste cinque terne (nella foto, uno dei rettangoli ha vertici nei 4 vertici rossi, un altro in quelli bianchi, un altro in quelli neri), ci accorgiamo anche che i tre rettangoli giacciono su tre piani a due a due ortogonali fra loro.

Questo rende naturale sceglierli come i tre piani coordinati di un sistema di riferimento, il che permette di risolvere in maniera semplice un problema che a primo impatto potrebbe apparire complicato, cioè quello di determinare delle coordinate per i vertici dell’icosaedro. Se scegliamo l’unità di misura in modo che lo spigolo dell’icosaedro sia di lunghezza 2, allora i quattro vertici che appartengono al piano z=0 avranno coordinate (±1,±τ,0) (oppure (±τ,±1,0), a seconda di come vengono scelti gli assi x e y).
Abbiamo qui indicato con τ il rapporto aureo, cioè il rapporto fra diagonale e lato di un pentagono regolare, che vale τ=(1+√5)/2.
Si può procedere analogamente per le altre due quaterne di vertici sui piani y=0 e x=0 rispettivamente, con la differenza che questa volta non possiamo più scegliere: se abbiamo fissato la prima quaterna come (±1,±τ,0), le altre due quaterne saranno (0,±1,±τ), (±τ,0, ±1), cioè quelle ottenute dalla prima permutando ciclicamente le coordinate. L’altra scelta per i primi quattro vertici avrebbe portato ai dodici punti di coordinate (±τ,±1,0), (0,±τ,±1), (±1,0,±τ).
Ma che cosa possiamo “leggere” nelle coordinate? E come facciamo a leggere queste informazioni?
Possiamo immaginare che questo sistema di coordinate corrisponda ad appoggiare l’icosaedro su un tavolo (in equilibrio instabile!) su uno spigolo, in modo che sia perpendicolare al tavolo la retta passante per i punti medi di due spigoli opposti; in questo modo i piani orizzontali sono i piani individuati da punti che hanno uguale la terza coordinata. Se cerchiamo di capire cosa succede “affettando” l’icosaedro con dei piani orizzontali, e in particolare su quanti e quali di questi piani sono ubicati i dodici vertici, otteniamo una situazione di questo tipo:
• ci sono due vertici sul tavolo (nella posizione più bassa possibile), con la terza coordinata uguale a -τ: nella foto si può immaginare che siano due vertici bianchi;
• ci sono poi due vertici con terza coordinata uguale a -1: nella foto, ci riferiamo a due vertici rossi;
• risalendo troviamo, a metà strada, quattro vertici alla stessa altezza, con terza coordinata z=0: nella foto, sono i vertici in nero;
• risalendo ancora, troviamo due vertici con terza coordinata z=1: nella foto sono gli altri due vertici in rosso, che insieme ai precedenti sono vertici del rettangolo aureo messo in evidenza;
• infine gli ultimi due con terza coordinata z=τ: nella foto sono gli altri due vertici bianchi.
Naturalmente, si ottiene la stessa cosa se studiamo come si dispone l’icosaedro rispetto agli altri due assi coordinati (dopotutto, la simmetria vuol ben dir qualcosa!).

Proviamo ora a cambiare punto di vista e a immaginare l’icosaedro, in equilibrio ancora più instabile, su un vertice. Magari possiamo appenderlo a un filo. “Vediamo” allora chiaramente che i suoi vertici si dispongono su 4 piani paralleli: due estremali, che contengono un vertice ciascuno (giallo e nero nella foto) e altri due che contengono cinque vertici ciascuno (rispettivamente, rossi e bianchi nella foto). Potremmo leggere questo fatto geometrico dalle coordinate? Naturalmente dovremo cambiare sistema di riferimento se vogliamo che questi quattro piani appaiano come quattro piani orizzontali (di equazione z=costante); possiamo però in alternativa tenerci questo sistema di riferimento, e quindi le coordinate che già abbiamo trovato, e ottenere questa situazione “affettando” l’icosaedro con piani, tutti paralleli fra loro, ma non più orizzontali.

Scegliamo allora un vertice (e va bene uno qualsiasi! Di nuovo, la simmetria è preziosa!), per esempio P=(1,τ,0), e il suo opposto Q=(-1,-τ,0), e pensiamo a questi due vertici come polo Nord e polo Sud (vertice giallo e vertice nero nella foto; la direzione che sostituisce la direzione verticale è allora la direzione che li collega ed è parallela al vettore
(1,τ,0) - (-1,-τ,0) = (2,2τ,0) = 2(1,τ,0).
Con un po’ di geometria analitica, non è difficile convincersi del fatto che i piani perpendicolari alla direzione individuata da un certo vettore (a,b,c) sono proprio i piani di equazione
ax+by+cz = costante.
Quindi, nel nostro caso, i piani con cui vogliamo “affettare” l’icosaedro sono i piani perpendicolari alla direzione individuata dal vettore (1,τ,0), cioè i piani di equazione x+τy=costante.
Per trovare qual è questa costante per i diversi vertici dell’icosaedro, basta sostituire in x+τy le coordinate corrispondenti a un vertice. Anche prima di fare i conti, sappiamo cosa aspettarci: un valore minimo (in corrispondenza al vertice Q, nero nella foto), un valore massimo (in corrispondenza al vertice P, giallo nella foto), e due valori intermedi, ciascuno dei quali è ottenuto cinque volte.
Proviamo allora a fare i conti: il valore minimo k_Q, realizzato nel punto Q corrisponde a
x+τy = -1+τ(-τ) = -1-τ² = -1-(τ+1) = -τ-2
Stiamo qui usando che per il rapporto aureo τ vale τ² = τ+1.
Il valore massimo k_P realizzato nel punto P corrisponde a
x+τy = 1+τ(τ) = 1+τ² = 1+(τ+1) = τ+2.
Negli altri due punti dove si annulla la terza coordinata, ossia A=(-1, τ,0) e B= (1,-τ,0), abbiamo rispettivamente
k_A = x_A+τy_A = -1+τ² = -1+(τ+1) =τ
k_B = x_B+τy_B = 1-τ² = 1-(τ+1) =-τ
E negli altri otto? Per quattro di questi otto (±τ,0,±1) la seconda coordinata è 0 e quindi x+τy non è altro che la prima coordinata, cioè τ per due vertici e -τ per gli altri due; per gli altri quattro vertici (0,±1,±τ) è nulla la prima coordinata e quindi x+τy rappresenta la seconda coordinata (±1) moltiplicata per τ, ovvero, come prima, τ per due vertici e -τ per gli altri due.
In conclusione, abbiamo ritrovato dalle coordinate quello che già ci aspettavamo di trovare, cioè che i dodici vertici dell’icosaedro si dispongono su quattro piani paralleli:
• uno (in giallo nella foto) , (1, τ,0), sul piano x+τy = τ+2;
• cinque (in rosso nella foto), e precisamente (-1,τ,0), (τ,0,1), (τ,0,-1), (0,1,τ), (0,1,-τ), sul piano x+τy = τ;
• cinque (in bianco nella foto), e precisamente (1,-τ,0), (-τ,0,1), (-τ,0,-1), (0,-1,τ), (0,-1,-τ), sul piano x+τy = -τ;
• uno (in nero nella foto), (-1,-τ,0) sul piano x+τy = -τ-2.

La situazione diventa ancora più interessante se appoggiamo l’icosaedro al tavolo su una faccia (in equilibrio finalmente stabile!). Osservandolo, vediamo che anche questa volta i suoi vertici si dispongono lungo quattro piani paralleli, ma ora ciascun piano contiene tre vertici e, di più, tre vertici che formano un triangolo equilatero.

Quindi i dodici vertici dell’icosaedro si dispongono su 4 triangoli equilateri, di cui due più piccoli (due facce opposte del poliedro) e due più grandi. Possiamo anche dire quanto più grandi? Tornando all’osservazione del modello, è facile ritrovare il lato del triangolo più grande come diagonale di un pentagono regolare che ha come lato lo spigolo dell’icosaedro (ovvero il lato del triangolo più piccolo). Quindi il rapporto di similitudine fra i due triangoli è… il rapporto aureo!

Cerchiamo, anche in questo caso, di ritrovare lo stesso risultato usando le coordinate. Questa volta i piani con cui dobbiamo “affettare” l’icosaedro sono i piani paralleli a una faccia, quindi la prima difficoltà che incontriamo è quella di trovare come si può scrivere il piano di una faccia. Lasciamoci aiutare (ancora!) dalla simmetria, osservando che nelle coordinate dei vertici si “vede” una simmetria di ordine tre che corrisponde a una permutazione ciclica delle coordinate e che possiamo immaginare corrisponda, nell’icosaedro stesso, a una rotazione di ordine tre e quindi rispetto a un asse perpendicolare a due facce opposte. Allora la direzione Sud-Nord che stiamo cercando può essere questa volta la direzione del vettore (1,1,1) e i piani ortogonali a questa direzione sono i piani del tipo x+y+z = costante.
E in effetti, secondo questa direzione, troviamo:
• tre punti sul piano x+y+z =τ+1; i punti (1,τ,0), (τ,0,1), (0,1,τ): i vertici bianchi nella foto;
• tre punti sul piano x+y+z =τ-1; i punti (-1,τ,0), (τ,0,-1), (0,-1,τ): i vertici neri nella foto;
• tre punti sul piano x+y+z =-τ+1; i punti (1,-τ,0), (-τ,0,1), (0,1,-τ) i vertici rossi nella foto;
• tre punti sul piano x+y+z =-τ-1; i punti (-1,-τ,0), (-τ,0,1), (0,1,-τ): i vertici gialli nella foto.
Tutto molto simmetrico! E tutto molto aureo!

E se vogliamo ritrovare anche il rapporto fra i lati dei due triangoli ci basta un piccolo conto; per esempio, la lunghezza del lato del triangolo piccolo, elevata al quadrato, è
(τ-1)²+τ²+1 = τ²-2τ+1+τ²+1 = τ+1-2τ+1+τ+1+1 =4,
cioè il lato ha lunghezza 2 (cosa che peraltro sapevamo già, perché avevamo fissato all’inizio l’unità di misura del sistema di riferimento in modo che lo spigolo dell’icosaedro avesse lunghezza 2).
La lunghezza del lato del triangolo grande si può ritrovare, per esempio, come la distanza fra i due punti (-1,τ,0), (τ,0,-1); calcolando la distanza al quadrato si ottiene
(-1-τ)²+τ²+1 = τ²+2τ+1+τ²+1= τ+1+2τ+1+τ+1+1 =4τ+4 = 4(τ+1) = 4τ²
cioè il lato del triangolo più grande ha lunghezza 2τ, e il rapporto fra i due è, come già sapevamo, proprio il rapporto aureo.
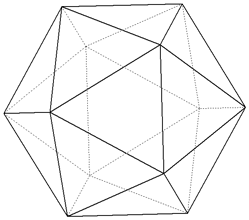
Possiamo sfruttare questa costruzione per disegnare un icosaedro (in proiezione parallela); infatti, proiettando su un piano x+y+z=k (che corrisponde poi a guardare “dall’alto” un icosaedro appoggiato a terra su una faccia), i dodici vertici dell’icosaedro si dispongono su due esagoni regolari, concentrici, uno più grande e uno più piccolo, con rapporto di similitudine che è proprio il rapporto aureo. E, una volta segnati i vertici (e sapendo come è fatto il poliedro) è facile ricostruire come debbano essere messi gli spigoli.
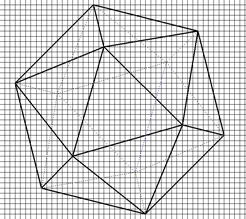
Si può anche sfruttare il fatto che il rapporto fra due numeri di Fibonacci consecutivi (2, 3/2, 5/3, 8/5, 13/8, …) tende al rapporto aureo τ per disegnare un icosaedro (quasi!) regolare sulla carta a quadretti: e qui il “quasi” proviene da due (diverse!) approssimazioni; in primo luogo il fatto che (non è possibile disegnare un triangolo equilatero sulla carta a quadretti, ma) si può disegnarne una buona approssimazione, e quindi anche una buona approssimazione di un esagono regolare; in secondo luogo il fatto di aver approssimato τ con una frazione (in figura l'approssimazione usata è 5/3, che è già sufficiente per ottenere una bella immagine).

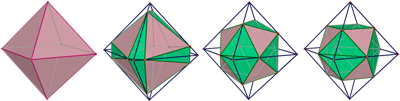
Per concludere, ecco un’altra costruzione in cui è coinvolto l’icosaedro e il rapporto aureo, e che può costituire una maniera per costruire un icosaedro a partire da un poliedro più semplice, cioè l’ottaedro regolare. L’ottaedro ha 12 spigoli, uno per ciascun vertice dell’icosaedro; verrebbe voglia di scegliere un vertice per spigolo, ma come? La maniera più naturale sembra essere quella di scegliere il punto medio di ogni spigolo; si ottiene così un bel poliedro, ma non l’icosaedro, bensì un cubottaedro; che, fra l’altro, si potrebbe ottenere con la stessa costruzione anche a partire da un cubo (scegliendone i punti medi degli spigoli, che sono ancora 12). Torniamo però ai 12 spigoli dell’ottaedro, su cui vogliamo piazzare 12 punti in modo da ottenere i 12 vertici dell’icosaedro; e se non li mettiamo nei punti medi, dove mai potremo metterli? La risposta è a questo punto quasi obbligata…! Si tratta dei punti che dividono gli spigoli in rapporto aureo. Bisognerà fare un po’ attenzione, perché troveremo due punti di questo tipo: possiamo scegliere come vogliamo il primo, ma poi tutti gli altri andranno scelti in maniera coerente in modo per esempio che su ogni faccia (dell’ottaedro) i tre vertici scelti sugli spigoli siano a loro volta vertici di un triangolo equilatero.