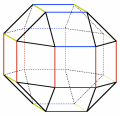
Uniform Polyhedra
Regular polyhedra are polyhedra where vertices, edges and faces can not be distinguished. This requirement is so strong that there are only five regular polyhedra. At any rate, other polyhedra - although not regular - can strike us for their symmetry.

Here on the left you may see football and, below, a polyhedron with the same structure. It is not a regular polyhedron because the faces are not all equal - there are hexagons and pentagons. Yet, it does have a symmetry. The faces - although not all alike - are regular polygons. Moreover, if we look at a vertex, we realize that at each vertex there are a pentagon and two hexagons. We can imagine to make a plaster cast around a vertex and obtain a sort of three-dimensional "stamp", which can be adapted to any other vertex.

The football is an example of a uniform polyhedron, i.e., a polyhedron which has faces that are regular polygons and all vertices can not be "distinguished". This latter property allows one to identify the uniform polyhedra with numerical symbols, which represent the polygons adjacent to every vertex. For instance, (5,6,6) is the symbol of the football.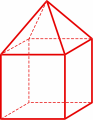
We could not use a symbol of this type for the polyhedron here on the right. Indeed, it has vertices with four triangles, others with two squares and two triangles, and others with three squares.
What do we mean by saying that the vertices can’t be distinguished? After all, vertices are points and,
undoubtedly, all points are equal! Already the example of the "three-dimensional stamp" tells us something about all the faces adjacent to a vertex and not only the vertex!
Actually, the problem is even subtler, and to say that the vertices can’t be distinguished, it is not even enough that a three-dimensional "stamp" adapts to any vertex with the same arrangement of faces.
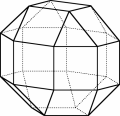
The polyhedron on the right (the Miller polyhedron) has three squares and an equilateral triangle at every vertex; so a convenient three-dimensional "stamp" would adapt to any vertex. Yet, the vertices can be distinguished!
It is possible to see it by looking at the chain of squares that rounds the "equator" of the polyhedron. There is just one chain of this type because, if we start from other pairs of adjacent squares , we can’t make a full round. So, two vertices may be distinguished because they do not have the same position with respect to this chain like, for instance, the two vertices A and B. 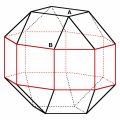
It is impossible to move the polyhedron so that the vertex A maps to the vertex B and the polyhedron stays in the same position.
The other polyhedron you may see below "looks like" the Miller polyhedron quite a lot, but it is "more symmetric". There are three chains of squares and each vertex belongs to two of these three chains. With a little bit of patience, you may verify that the same three-dimensional "stamp" adapts to any vertex. Furthermore, for any two vertices there exists a symmetry of the polyhedron which maps the two vertices one onto the other. This is the requirement which must be fulfilled to talk about a uniform polyhedron (and to denote it by the symbol (3,4,4,4)).