Regular polyhedra

When we throw a die we expect, since its shape is evidently symmetric, that any of the six numbers marked on its faces has the same probability to appear.

In some toy shops, besides the usual six-faced dice, you can also buy dice with four, eight, twelve e twenty faces.

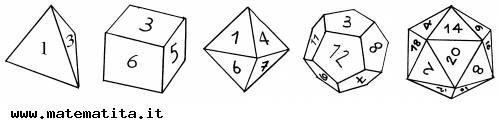
What is special about the five polyhedra represented by these dice? To see what properties they have, we first consider some other examples of polyhedra.

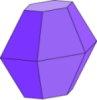
We could build a die from a geoid, for example. Such a polyhedron could even seem more "regular" than the five dice above since its shape is "closer" to that of a sphere, but, if we study it carefully, we notice that its vertices are not all of the same type: at some vertices (like A) five edges radiate and so five triangles come together; at others (like B) six edges start and so six triangles meet.

We call a polyhedron regular if all its faces are equal regular polygons and the same number of faces meet at every vertex. In such a polyhedron all the faces, edges and vertices are indistinguishable.

None of the polyhedra in the second figure above is regular, while the five dice are all examples of regular polyhedra. Are there any more? (After all, in the plane we can build regular polygons with as many edges as we like.) The answer is: no. In space, there are only the five regular polyhedra of the diceshown in the first figure.

Even the ancient Greeks knew this fact; it so impressed them that the Pythagoreans, and later Plato, built their cosmogonical theories on it, associating the fundamental constituents of nature to the five regular polyhedra. Because of this, the regular polyhedra are also called Platonic solids.

In his `Timaeus', Plato describes the tetrahedron as "element and germ" of fire, the octahedron of air, the icosahedron of water, the cube of earth, and the dodecahedron represents the image of the entire universe: "There still remained a fifth construction, which the god used for embroidering the constellations on the whole heaven".
The last book of the Euclid's "Elements" is dedicated to the five Platonic solids, to some of their properties and relationships, and to the proof that there are no other regular polyhedra.

Models of regular polyhedra have been found from pre-Greek civilisations. The harmony of their proportions and their mathematical properties give them a charm that has been captivating artists and scientists ever since.
Dodecahedra had a religious meaning in the Etruscan civilisation, and were also used as dice by the Romans.
In the Renaissance, regular polyhedra were used as a good subject for studies of perspective: we can find them in works by Paolo Uccello, Piero della Francesca, Albrecht Dürer, Leonardo da Vinci, Luca Pacioli and Leonardo Pisano (also known as Fibonacci).

In 1595 Kepler believed that he had "penetrated the secrets of the Creator" because he had elaborated a model of a planetary system (that later became discredited) by using the Platonic solids to describe the distances between the elliptic orbits of the six planets then known.

Shapes inspired by regular polyhedra are also common in modern art and design, from works of Escher to modular architecture, to objects by Munari.
One last curiosity: in France they built dodecahedral bottle banks.

Even nature shows us examples of regular polyhedra: some cristals , viruses which often have icosahedral form, simple living organisms like radiolaria, ...