 The borromean rings are the symbol of the famous Borromeo family (and of various others). They can be found around Milan and in Lombardy in various places, on effigies and statues, on doors and fountains. What do knots and links have to do with these rings?
The borromean rings are the symbol of the famous Borromeo family (and of various others). They can be found around Milan and in Lombardy in various places, on effigies and statues, on doors and fountains. What do knots and links have to do with these rings?
 Let us take three strings and weave them into the braid is depicted here. If you join the ends of each string, you will obtain the borromean rings, which provide an example of a link with three components.
Let us take three strings and weave them into the braid is depicted here. If you join the ends of each string, you will obtain the borromean rings, which provide an example of a link with three components.
 These rings have a very particular property, which conceals a symbolic meaning. If you remove one of the three rings, the other two can be separated. All three together, however, cannot be separated.
These rings have a very particular property, which conceals a symbolic meaning. If you remove one of the three rings, the other two can be separated. All three together, however, cannot be separated.
This does not happen for any "copy" of the Borromean rings, that is, for any link with three components with the same "shadow" as that of the Borromean rings. In fact, the link obtained depends on the under/over choices you make for each crossing. To tell the truth, while you indeed sometimes find "real" Borromean rings around Milan, you can also find some false rings, which appear to be the same, but have some inverted crossings. In this poster from the exhibition matemilano you find all five possible combinations, the Borromean rings included.
One of these combination has the following property: if you remove one of the three rings, the other two remain linked (they form a chain of two rings).
This link belongs to the family of links that can be drawn on the surface of a torus. More precisely, it is a torus link (3,3): see the information site Two Numbers for a knot.
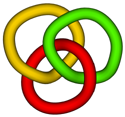 Another "imitator" can be manipulated into a chain with three rings. If you remove the red ring, the other two are free. If you remove the yellow or the green ring, the other two remain linked (they form a chain of two rings).
With this link it is possible simply to remove one of the three rings, while the other two remain linked.
Another "imitator" can be manipulated into a chain with three rings. If you remove the red ring, the other two are free. If you remove the yellow or the green ring, the other two remain linked (they form a chain of two rings).
With this link it is possible simply to remove one of the three rings, while the other two remain linked.
Finally, this is the unlink with three components: each component is not linked with the other two.
There are no other "imitators" of the borromean rings. Start from the diagram which represents their shadow (with the three intersecting circles). If you decide which branch overcrosses or undercrosses at each of the six crossings, you come up with one of the six links above. This does not mean that there are no other diagrams besides the ones in this page. There are six crossings. For each crossing you have an under/over choice; so you have 26=64 possibilities. Because of symmetry arguments, it is easy to see that the diagrams are just 10. Among them, some give the same link with three components. The five cases described above give all the possibilities.
 The real borromean rings have another property. Their "imitators" are very flexible: one of them (the unlink with three components), is so "flexible" that each ring can be moved as freely as you wish. The borromean rings, in contrast, are very "rigid". In particular, they cannot be constructed with plane circles. This was known to the artisans who reproduced them on bas-reliefs and in cast iron. For example, you can make a rigid model with three plane ellipses that are not circles. If you make a model of them with (flexible) rings, you can form each of them (one at a time) into a circular shape. If you try to do this by laying all three together (by "flattening" them in order to get the diagrams on the poster), you will find that it is impossible: the three rings cannot be laid flat (and they are not circles). It is also interesting to observe that the Borromean rings can be represented in various "symmetric" ways: for instance, they can be made with three plane curves in three mutually perpendicular planes.
The real borromean rings have another property. Their "imitators" are very flexible: one of them (the unlink with three components), is so "flexible" that each ring can be moved as freely as you wish. The borromean rings, in contrast, are very "rigid". In particular, they cannot be constructed with plane circles. This was known to the artisans who reproduced them on bas-reliefs and in cast iron. For example, you can make a rigid model with three plane ellipses that are not circles. If you make a model of them with (flexible) rings, you can form each of them (one at a time) into a circular shape. If you try to do this by laying all three together (by "flattening" them in order to get the diagrams on the poster), you will find that it is impossible: the three rings cannot be laid flat (and they are not circles). It is also interesting to observe that the Borromean rings can be represented in various "symmetric" ways: for instance, they can be made with three plane curves in three mutually perpendicular planes.