In the following virtual leaflets you may find some FAQ on the exhibition Diving into the fourth dimension, which was held during the Festival della Scienza in Genova, 2007.

Imagine you are walking in a wood, far from any man-made structure. Among the large variety and complexity of shapes around you, you will see some repeated forms. Regularities and symmetries start to appear. Even with the continuous change of nature, some things seem to be preserved, some directions of growth, or designs, seem to be favoured.

From any wood you can see the sun as round as the full moon, rain falling in approximately spherical drops, or snow falling in hexagonal crystals.
The tree-trunks and mushrooms have rotational symmetry about a central axis. Flowers often have rotational symmetry of pentagonal, square or hexagonal type... Many insects, mammals and leaves have bilateral symmetry. Millepedes, blades of grass, or the leaves of ferns display the beginnings of translational symmetry..

These symmetries are hardly ever perfect: the leaves of a four-leaved clover are not exactly equal, so its symmetry is not as precise as that of a square. However, we will not be too bothered about this and say coolly that a star fish has pentagonal symmetry even if one of its five arms is folded or broken.

Having awakened our curiosity, we can make some hypotheses about how and why nature is organised in symmetric shapes, hypotheses linked to criteria such as functionality, replacement, locomotion, or economy.

A system evolves interacting with its environment and, if the external conditions that impose on it a particular effect have some symmetry, then the result may display, completely or partially, the symmetry of the cause that produced it. The Earth is not perfectly spherical because its rotation causes it to bulge out around the equator and so become flattened at the poles. However, the rotational symmetry about its axis and reflection symmetry with respect to the equator is preserved.

Crystals are a notable example of regularity in the inorganic world. The crystals of salt, iron oxide and pyrite are respectively of cubic, octahedral, and dodecahedral shape. It is likely that the pyrite crystal suggested the dodecahedral shape to the ancient Greeks, who found it in Sicily, where it is abundant.

Symmetrical structures can have advantages for living organisms. They are stable, compact, homogeneous, and interchangeable. As in a production line in a factory, they reproduce themselves more easily and quickly. A spherical body disperses less heat because a smaller surface area is needed to separate it from outside.

As living organisms evolved, they lost the high degree of symmetry that is characteristic of lower orders. Many unicellular organisms, like the simplest ones suspended in water, are as symmetrical as possible, that is they have a spherical shape.
More complex sea organisms, creatures like starfish or jellyfish, or plants that are fixed to the ground where they grow, are conditioned by the direction of gravity: their upper and lower parts are different, but they still have rotational symmetry about a (vertical) axis.

In higher organisms that move by themselves, like fish or mammals or birds, we can also distinguish the front (where the eyes are) from the back. But these creatures often preserve bilateral symmetry. This is favoured by linear motion and acts against helical motion (like a screw).

Even the human body has substantially bilateral symmetry. The embryo initially develops a repetitive translational structure. Such symmetry is then lost when the organs such as the heart or liver, of which we have only one copy, develop and position themselves off the central axis, or when the intestine, as it needs to lengthen, folds itself up.

Some crustaceans break their bilateral symmetry by developing one claw more than the other. If the largest claw is lost, a new one is generated in its place, while the other grows and becomes the largest one. The two possible shapes are reflections of each other.

Translational symmetry is a property that applies only to unbounded figures. But a structure that grows in only one direction by repeatedly adding the same unit, like an ear of wheat, or an earthworm, is potentially symmetric with respect to translation: as time passes, new segments equal to the previous ones grow.

The need to fill all available space with the same unit gives rise to numerous symmetrical situations, for example the hexagonal structure of honeycomb, the tetrahedral symmetry of a foam of soap bubbles, the pigment of the retina in our eyes, or the polyhedral shape of some vegetable cells like those in the heart of a tree trunk or in the structure of some diatoms.

The 48 symmetries of the cube form a family with interesting properties. It is a very closed family: the result of the composition of two or more elements of the family is still a member of the family.

The identity transformation has an exceptional role in it. It is the neutral element of the family, in the sense that any symmetry of the cube composed with the identity remains itself.

In general the order in which you compose the transformations affects the final result.
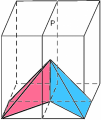
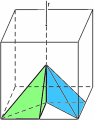
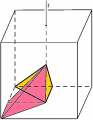
For example, in the two figures on the left we see where the reference pyramid moves if we first reflect the cube with respect to the plane p and then we rotate it of 1/4 of turn about the line r. In the other two figures on the rigth, we see where the pyramid moves if we reverse the order of composition.

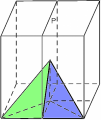Any symmetry of the cube has a mischievous twin with which it has a privileged relationship. The mischievous twin undoes the symmetry by moving the reference pyramid back to the start. It is called the inverse of the symmetry. When a symmetry is combined with its inverse, independent of the order, the result is the identity. For example, the rotation of 1/4 of turn about the line r has as its inverse the rotation of 3/4 of turn about r; any reflection is its own inverse; the composition represented in the figures above, reflection in the plane p followed by a rotation of 1/4 of turn about r, has as its inverse the composition of a rotation of 3/4 of turn about r followed by reflection in the plane p -- in this order! This is the same as when you reverse the operation "put on socks then put on shoes", first you take off shoes then you take off socks, not vice versa!

Any symmetry of the cube composed with itself a certain number of times gives the identity. For example, the reference pyramid goes back to its initial position if we perform four times a rotation of 3/4 turn about a line joining the centres of two opposite faces, or if we repeat twice a reflection in a mirror plane.

In describing the characteristics of the family of symmetries of the cube we have given an example of one of the most important concepts in mathematics: the structure known as a group.
The symmetries of the cube, with the operation given by performing first one and then the second (composition), constitute a group. Another example of group is given by the set of (positive and negative) integers, with the operation of sum.
This family too is closed (the sum of two integers is still an integer); the number 0 has the same role as the identity transformation has for the family of symmetries of a cube (the sum of any number and zero is equal to the starting number); and for any number, its relative with which it has a privileged relationship is the number of opposite sign (any number summed with its opposite is zero).

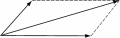The group structure is found in many other contexts: for example, the set of vectors in the plane with the combination rule given by the parallelogram rule for the sum of two vectors is a group.

Not only the symmetries of a cube, but also the symmetries of any plane figure or of any solid object form a group with the operation of composition, just like in the case of the cube.
If the starting shape is completely asymmetric, the symmetry group is the group containing a single element: the identity.

The symmetry group of the plane figure on the left has 6 elements. (Which ones? What is the inverse of each element?)

Rosettes are plane figures whose symmetry group contains a finite number of elements. There are also some figures whose symmetry group contains infinitely many elements, for example a circle or a straight line.

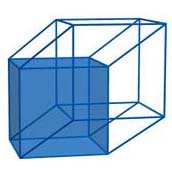
In each representation of a hypercube you should “see” each of the eight cubic faces of the hypercube. This is clear for a net, but what about a Schlegel diagram and a projection? Where are the eight cubes?

In a Schlegel diagram, you can see that seven out of the eight cubic faces of a hypercube are represented. A small cube inside and other six deformed cubes - which are glued face to face - and form the big cube outside. Where is the eighth cube? The faces of the eighth cube are the faces of the big cube. Since the interior of the big cube is already “taken” by the other seven cubes, we can imagine that the interior of the eighth cube is the exterior of the big cube, which is an unlimited region!
This remark comes from our way of thinking in three dimensional space. The Schlegel diagram of the cube in the plane can help us understand the hypercube.
We notice that also in a Schlegel diagram of a cube a face is missing. It is the face delimited by the big square. Actually, this is a two-dimensional projection. In fact, we should realize that the other five faces are in close-up (like a relief) with respect to the sixth face, the one delimited exactly by the edges of the big square.
Likewise, in the diagram of a hypercube the seven cubes, which are inside, must be imagined in “close-up” with respect to the cubic face delimited by the big cube. This perspective is less evident than in the case of a cube because we are adding a dimension to our three-dimensional space to highlight what is in the big cube; but this is “watching” in a four-dimensional space…
As for a perspective projection of a hypercube two cubes are easily detectable. Where are the others? Let us consider a projection of a cube on the plane. The projection of the six faces are intertwined. In the same vein, the projection of the eight cubic faces of a hypercube intersect each other. To observe them, let us consider the bases of these two cubes.

You can easily see that they are the bases of two other solids (first, second) with eight vertices and twelve edges, which are the projection of two other cubic faces.
There are still four cubes missing: we leave it to the reader to discover where they are “hidden”……

Why do we need eight cubes for a net of a hypercube?
To understand it, let us examine the cases of a square and a cube:

• For a square each edge is adjacent to other two. The two vertices of these two edges, which are not in common with the original one, are the vertices of the edge opposite to the original one. The number of the edges is thus 1+2+1=4 (the first one, the two adjacent ones and the opposite one);
• For a cube each square is adjacent to other four squares (it has four edges); the “free” edges of these four squares are the edges of the square opposite to the original one. The number of the faces is thus 1+4+1=6 (the original face, the four adjacent ones and the opposite one).

Both in the case of a square and a cube, we have the following situation: each ”face” (an
edge or a square respectively) is adjacent to “almost” all the other faces, that is all except one of them.

Let us try to proceed by analogy for a hypercube. Since each “face” of a hypercube is a cube, with six faces, it is reasonable to think that there are 1+6+1=8 cubic faces of a hypercube (a cube, the six adjacent cubes and the opposite cube). We are led to assume that a hypercube has eight cubic faces.

How many cubes are there really in a hypercube? Infinitely many!


To understand this statement, let us consider again a cube and proceed by analogy.

A cube has six faces, which are identical. Actually, there are infinitely many squares in a cube. For example, let us consider a cube and a plane parallel to a face. If we imagine to let the cube pass through the plane, the intersection of the plane and the cube is a square at every time.

MANCA UN PEZZO!!!
Allo stesso modo immaginate un ipercubo che attraversi un universo tridimensionale come il
nostro, che sia parallelo a una delle sue otto facce cubiche: l’intersezione
dell’universo 3d e dell’ipercubo è un cubo e quindi ad ogni istante apparirebbe come un cubo.

A cura di Paolo Bellingeri per la mostra Un tuffo nella quarta dimensione.