Biforcazione e Catastrofe
Biforcazione
Sistema ad un grado di libertà 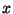 soggetto al potenziale
soggetto al potenziale
Le posizioni d'equilibrio del sistema sono date da
quindi se 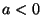 c'è una sola posizione d'equilibrio (
c'è una sola posizione d'equilibrio (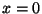 ) che è stabile
(i.e. è un minimo del potenziale), mentre se
) che è stabile
(i.e. è un minimo del potenziale), mentre se 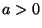 ci sono tre distinte posizioni d'equilibrio (
ci sono tre distinte posizioni d'equilibrio (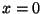 ,
, 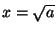 e
e
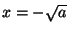 ) due stabili (
) due stabili (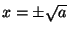 ) ed una instabile (
) ed una instabile (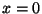 ).
).
In 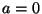 si ha una biforcazione (prima c'è una sola posizione d'equilibrio
stabile, poi ce ne sono due) e si noti che la soluzione che per
si ha una biforcazione (prima c'è una sola posizione d'equilibrio
stabile, poi ce ne sono due) e si noti che la soluzione che per 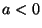 era
stabile passando attraverso il punto di biforcazione diventa instabile.
era
stabile passando attraverso il punto di biforcazione diventa instabile.
Nella prima parte dell'animazione il pallino blu descrive il valore del
parametro 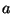 mentre l'ordinata del pallino arancio descrive la
posizione d'equilibrio occupata dalla palla rossa sul grafico di
mentre l'ordinata del pallino arancio descrive la
posizione d'equilibrio occupata dalla palla rossa sul grafico di 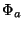 . La
``forchetta'' che compare alla fine della prima parte rappresenta l'insieme
delle posizioni d'equilibrio al variare del parametro
. La
``forchetta'' che compare alla fine della prima parte rappresenta l'insieme
delle posizioni d'equilibrio al variare del parametro 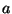 .
.
Catastrofe
Sistema ad un grado di libertà 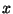 soggetto al potenziale
soggetto al potenziale
Introducendo un altro parametro (il potenziale precedente è un caso
particolare di questo, infatti
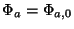 ) si riesce a girare attorno
al punto di biforcazione, si presenta però un'altro fenomeno: la
``catastrofe''.
) si riesce a girare attorno
al punto di biforcazione, si presenta però un'altro fenomeno: la
``catastrofe''.
Le posizioni d'equilibrio del sistema sono date da
questo è un generico polinomio di terzo grado (a meno di una traslazione,
ogni polinomio di terzo grado ha questa forma) quindi ci saranno valori di 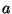 e
e 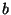 per i quali c'è un'unica radice che sarà un minimo del potenziale e
ci saranno valori per cui si hanno tre radici distinte che si può facilmente
vedere che sono due minimi (stabili) ed un massimo (instabile). Si può
provare che per
per i quali c'è un'unica radice che sarà un minimo del potenziale e
ci saranno valori per cui si hanno tre radici distinte che si può facilmente
vedere che sono due minimi (stabili) ed un massimo (instabile). Si può
provare che per
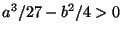 si hanno tre radici distinte e per
si hanno tre radici distinte e per
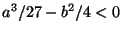 ce n'è una sola. Nel passaggio dalla zona con tre radici a
quella con una radice, si può avere la catastrofe: la posizione d'equilibrio
stabile in cui si trova il punto scompare e quindi il punto è costretto a
saltare sull'altra posizione d'equilibrio.
ce n'è una sola. Nel passaggio dalla zona con tre radici a
quella con una radice, si può avere la catastrofe: la posizione d'equilibrio
stabile in cui si trova il punto scompare e quindi il punto è costretto a
saltare sull'altra posizione d'equilibrio.
Nella seconda parte dell'animazione, il pallino blu si muove descrivendo una
circonferenza nello spazio dei
parametri 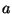 e
e 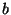 (il piano bianco) mentre la terza coordinata del pallino
arancio descrive la corrispondente posizione d'equilibrio occupata dalla palla
rossa sul grafico di
(il piano bianco) mentre la terza coordinata del pallino
arancio descrive la corrispondente posizione d'equilibrio occupata dalla palla
rossa sul grafico di 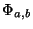 . La superficie rappresenta l'insieme delle
posizioni d'equilibrio al variare dei parametri
. La superficie rappresenta l'insieme delle
posizioni d'equilibrio al variare dei parametri 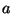 e
e 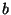 .
.
Sono disponibili anche la versione PostScript
(ps) a Portable Document Format (pdf) di
questa breve nota.
This document was generated using the
LaTeX2HTML translator Version 99.2beta8 (1.42)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
Luminati Domenico
2002-10-09
![]() soggetto al potenziale
soggetto al potenziale
![]() si ha una biforcazione (prima c'è una sola posizione d'equilibrio
stabile, poi ce ne sono due) e si noti che la soluzione che per
si ha una biforcazione (prima c'è una sola posizione d'equilibrio
stabile, poi ce ne sono due) e si noti che la soluzione che per ![]() era
stabile passando attraverso il punto di biforcazione diventa instabile.
era
stabile passando attraverso il punto di biforcazione diventa instabile.
![]() mentre l'ordinata del pallino arancio descrive la
posizione d'equilibrio occupata dalla palla rossa sul grafico di
mentre l'ordinata del pallino arancio descrive la
posizione d'equilibrio occupata dalla palla rossa sul grafico di ![]() . La
``forchetta'' che compare alla fine della prima parte rappresenta l'insieme
delle posizioni d'equilibrio al variare del parametro
. La
``forchetta'' che compare alla fine della prima parte rappresenta l'insieme
delle posizioni d'equilibrio al variare del parametro ![]() .
.
![]() soggetto al potenziale
soggetto al potenziale
![]() e
e ![]() (il piano bianco) mentre la terza coordinata del pallino
arancio descrive la corrispondente posizione d'equilibrio occupata dalla palla
rossa sul grafico di
(il piano bianco) mentre la terza coordinata del pallino
arancio descrive la corrispondente posizione d'equilibrio occupata dalla palla
rossa sul grafico di ![]() . La superficie rappresenta l'insieme delle
posizioni d'equilibrio al variare dei parametri
. La superficie rappresenta l'insieme delle
posizioni d'equilibrio al variare dei parametri ![]() e
e ![]() .
.